А 190,4 км В
> 61,8 км/ч t = 4 ч > ? км/ч
1) 61,8 · 4 = 247,2 (км) - проедет мотоциклист за 4 ч;
2) 247,2 - 190,4 = 56,8 (км) - проедет велосипедист за 4 ч;
3) 56,8 : 4 = 14,2 (км/ч) - скорость велосипедиста.
Выражение: (61,8 · 4 - 190,4) : 4 = 14,2.
1) 190,4 : 4 = 47,6 (км/ч) - скорость сближения при движении вдогонку;
2) 61,8 - 47,6 = 14,2 (км/ч) - скорость велосипедиста.
Выражение: 61,8 - 190,4 : 4 = 14,2.
Пусть х км/ч - скорость велосипедиста, тогда (61,8 - х) км/ч - скорость сближения при движении вдогонку. Уравнение:
(61,8 - х) · 4 = 190,4
61,8 - х = 190,4 : 4
61,8 - х = 47,6
х = 61,8 - 47,6
х = 14,2
ответ: 14,2 км/ч.
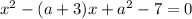
Воспользуемся теоремой Виета:
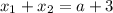
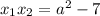
Произведение корней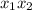 
на 2 больше суммы 
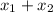этих корней, следовательно:
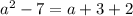
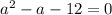
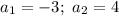
Определим, при каких значениях параметра 
данное уравнение существует.
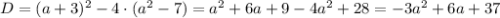
Следовательно,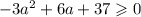 
— условие существования корней данного квадратного уравнения.
Проверим, удовлетворяют ли полученные значения параметров для решения исходного уравнения.
Если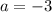 
, то получаем неправильное неравенство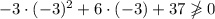 
Если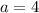 
, то получаем верное неравенство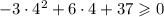 
Таким образом, только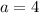 
обратит данное уравнение в таковое, что произведение корней на 2 будет больше суммы этих корней.
ответ: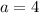
1)469,7:15.4=30.5
второе действие - сложение
2)30.5+9.52=40.02
3)161-40.02=120.98
4)120.98-1.5=119.48.