Найдите боковую поверхность конуса, в осевом сечении которого равнобедренный прямоугольный треугольник - id268350820200621 от ksenia376 21.06.2020 20:57

Question

Математика: Найдите боковую поверхность конуса, в осевом сечении которого равнобедренный прямоугольный треугольник с гипотенузой 6√2 см

ksenia376 · Accepted Answer

Рассмотрим функцию f(x)=(x-4)^6+(x-6)^6; уравнение принимает вид f(x)=64. Исследуем функцию на монотонность с производной:

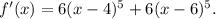f'(x)=6(x-4)^5+6(x-6)^5. Найдем нули производной:

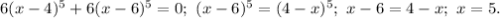
$6(x-4)^5+6(x-6)^5=0;\ (x-6)^5=(4-x)^5;\ x-6=4-x;\ x=5.$

Подставив в производную x=4<5, убеждаемся, что она отрицательна, то есть функция слева от 5 убывает. Подставив в производную x=6>5, убеждаемся, что она положительна, то есть функция справа от 5 возрастает. Следовательно, слева от 5 уравнение имеет не больше одного решения, точно так же справа от 5 уравнение имеет не больше одного решения. Эти решения легко угадываются: x=4 и x=6.

ответ: 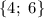$\{4;\ 6\}$

Замечание. Альтернативный решения - сделать замену x-5=t, после чего возвести (t-1) и (t+1) в шестую степень.

Найдите боковую поверхность конуса, в осевом сечении которого равнобедренный прямоугольный треугольник с гипотенузой 6√2 см

MOGZ ответил