ответ: 8 пар.
Объяснение:
Раскрыв скобки, получаем:
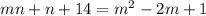
Перенесем слагаемые с переменными влево, а свободный член — вправо:
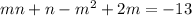
Из обеих частей уравнения вычтем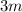 
:
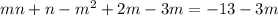
Разложим левую часть на множители методом группировки:
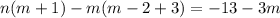
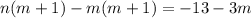
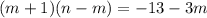
К обеим частям уравнения прибавим выражение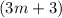 
:
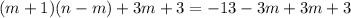
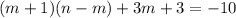
Вынесем общий множитель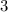 
за скобки:
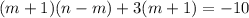
Вынесем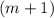 
:
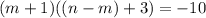
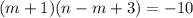
Так значения m и n целые (по нужному условию), значения выражений в скобках не могут быть дробными.
Произведение двух целых чисел равно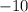 
в восьми случаях:
1) 
;
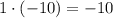2) 
;
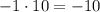3) 
;
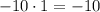4) 
;
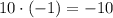5) 
;
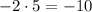6) 
;
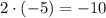7) 
;
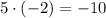8) 
.
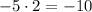Определим, какие будут значения m и n, если значения выражений в скобках равны множителям из каждого случая:
1) 
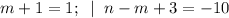
Получаем:
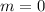
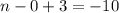
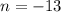
Значит, (m,n) = (0; -13).
Аналогично рассмотрим следующие случаи:
2) 
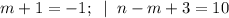
(m,n) = (-2; 5).
3) 
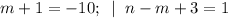
(m,n) = (-11; -13).
4) 
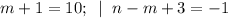
(m,n) = (9; 5).
5) 
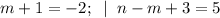
(m,n) = (-3; -1).
6) 
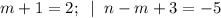
(m,n) = (1; -7).
7) 
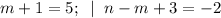
(m,n) = (4; -1).
8) 
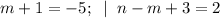
(m,n) = (-6; -7).
Выходит, 8 пар целых чисел (m, n) удовлетворяют данное равенство.
Пошаговое объяснение:
5/6 = 2х/3 4/9 = 8х/45 5х/12 = 2/3
2х * 6 = 3 * 5 8х * 9 = 45 * 4 5х * 3 = 12 * 2
12х = 15 72х = 180 15х = 24
х = 15 : 12 х = 180 : 72 х = 24 : 15
х = 1,25 х = 2,5 х = 1,6
6/7 = 10х/21 8/9 = 4х/27 27/5х = 9/16
10х * 7 = 21 * 6 4х * 9 = 27 * 8 5х * 9 = 27 * 16
70х = 126 36х = 216 45х = 432
х = 126 : 70 х = 216 : 36 х = 432 : 45
х = 1,8 х = 6 х = 9,6
24см/4=6см(сторона к.)
6см*6см=36cм^2