Вот несколько решений :
1. X=1
Y=1/3
2. X=2
Y=8/9
3. X=3
Y= 1
Теперь можешь построить график линейного уравнения с двумя переменными и увидеть все результаты, соответственно.
17
Пошаговое объяснение:
Объём пирамиды:
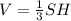 , где Н -высота пирамиды, S- площадь основания.
, где Н -высота пирамиды, S- площадь основания.
Высота пирамиды, половина диагонали основания - как катеты и боковое ребро - как гипотенуза образуют прямоугольный треугольник.
Обозначим половину диагонали как а, тогда квадрат бокового ребра равен:
Н²+а².
Найдем а.
Т.к. пирамида - правильная, то в основании лежит квадрат. Значит его сторона равна √16=4. А диагональ такого квадрата равна: √(4²+4²)=√32.
Значит а=√32/2
Найдем Н из формулы объёма пирамиды.
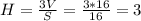
Тогда квадрат бокового ребра равен:
Н²+а² = 3² + 32/4 = 9+8 = 17.
12840 г краски
Пошаговое объяснение:
По условию задачи 1дм²=6 г краски. Тогда 10см²=6г, а 1см²=0,6 г краскиМы имеем 2 стороны бруска a*ba*b=60*70=4200см²(площядь стороны a*b)4200*0,6=2520 г (краски нужно для покраски 1 стороны a*b)2520*2=5040 г (краски нужно для покраски 2 сторон a*b)Мы имеем 2 стороны бруска a*ca*c=60*50=3000см²(площядь стороны a*c)3000*0,6=1800 г (краски нужно для покраски 1 стороны a*с)1800*2=3600 г(краски нужно для покраски 2 сторон a*с)Мы имеем 2 стороны бруска b*cb*c=70*50=3500см²(площядь стороны b*c)3500*0,6=2100 г(краски нужно для покраски 1 стороны b*с)2100*2=4200 г(краски нужно для покраски 2 сторон b*с) Чтобы покрасить весь брусок(6 сторон) нужно:5040+3600+4200=12840 г(краски)
y`=(x³/3ˣ)`=(3x²·3ˣ-x³·3ˣ·ln3)/(3ˣ)²
y`=0
3x²·3ˣ-x³·3ˣlnx=0
3ˣ·x²(3-x·ln3)=0
3ˣ>0 при любом х
х=0 или 3-x·ln3=0
х=0 или х=3/ln3
При переходе через точку х=3/ln3
производная меняет знак с + на - ,
значит в точке х=3/ln3 функция имеет максимум.
См. рис.
x=0 - точка перегиба, так как вторая производная меняет знак
y``=(6x·3ˣ+3x²·3ˣ·ln3-3x²·3ˣ·ln3-x³·3ˣ·ln²3)/(3ˣ)⁴
y=0 - горизонтальная асимптота, других асимптот нет.