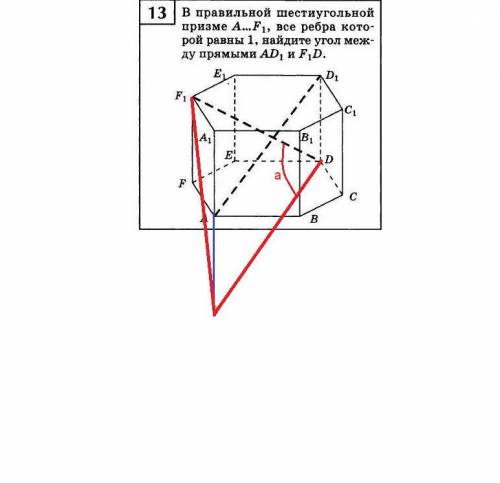
Геометрическое решение.
Применим перенос одного из отрезков так, чтобы их концы соединились.
Перенесём отрезок AD1 точкой D1 в точку D.
При этом точка А перейдёт в точку А2.
Получим треугольник DA2F1 с искомым углом D. Находим длины его сторон.
Сначала определим их проекции на основание.
AD = 1 + 2*(1*cos 60º) = 1 + 2*(1*(1/2)) = 2.
Тогда AD1 = √(2² + 1²) = √(4 + 1) = √5.
Находим DF = 2*(1*cos 30º) = 2*(1*(√3/2)) = √3.
Тогда DF1 = √((√3)² + 1²) = √(3 + 1) = √4 = 2.
И последний отрезок A2F1. Он равен:
A2F1= √(2² + 1²) = √(4 + 1) = √5.
Применим теорему косинусов.
cos D = (2² + (√5)² - (√5)²) / (2*2*√5) = 4/(4*√5) = √5/5 ≈ 0,4472.
Угол D = arccos(√5/5) = 1,1071 радиан или 63,435 градуса.
Примем за х кол-во деталей, кот . делает за час 2 рабочий.
первый делает х+3 детали
у первого уйдёт на заказ 340/(х+3) часов, у второго 340/х часов
у первого время на 3 часа меньше, составим уравнение:
340/х - 340/(х+3) = 3
(340(х+3) - 340х - 3 х(х+3) )= 0 (это числитель дроби, кот. получается при приведении к общему знаменателю, он равен нулю, при условии, что хне равен 0 и х не равен -3, ноэто невозможно по условию задачи
340х+1020-340х-3х^2-9x = 0
-3x^2-9x+1020 = 0
x^2+3x-340=0
D = 9+ 1360
D=1369
x= (-3+-37)/2
x= 17 или х=-20 (это невозможно по условию задачи)
ответ: 17 деталей делает 2 рабочий за час
2) 9+4=13 названий вспомнили девочки
3) 13-12=1 название девочки вспомнили больше
ответ: девочки вспомнили на 1 название больше чем мальчики