
1) Вычитаемое делится нацело на 25, значит и уменьшаемое должно делиться на 25
ответ: х-25 делится на 25 при х=50, х=250
2) 312:4=78. Первое слагаемое делится нацело на 4, значит и х должен нацело делиться на 4.
ответ: 312+х делится на 4 при х= 16 и х=40
3) 213 на 9 нацело не делится, значит х должен делиться нацело на 9.
ответ: 213х делится на 9 при х=9, х=18.
4) 5 нацело на 7 не делится, значит х должен делиться нацело на 7.
ответ: 5х делится на 7 при х= 49, х= 28
5) 5618 на 10 не делится. Признак делимости на 10: число должно оканчиваться нулём. 8+2=10, значит х равен любому числу оканчивающемуся на 2.
ответ: 5618+х делится на 10 при х = 42, х= 65782
6) 543 не делится на 2. Признак делимости на 2: число должно оканчиваться на чётную цифру (0, 2, 4, 6, 8). Но по условию разность не должна делиться на 5, значит она не может оканчиваться на 0, по признаку делимости на 5. Остаются варианты 2, 4, 6,8. Значит число х должно оканчиваться на 1, (543-1=542), 9 (543-9=534), 7 (543-7=536), 5(543-5=538)
ответ: 543- х делится на 2 но не делится на 5 при х= 49, х=5
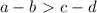
Всего есть 4 варианта увеличить числа: a и с, a и d, b и с, b и d.
Если увеличить числа а и с, то неравенство останется таким же с той лишь разницей, что к обоим частям прибавили по 1, истинность неравенства это не меняет.
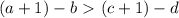
Аналогично, при увеличении чисел b и d обе части неравенства уменьшатся на единицу, но истинность неравенства останется такой же.
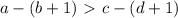
Если увеличить числа а и d, то левая большая часть станет еще большей, а правая меньшая часть станет еще меньше, таким образом, неравенство станет еще строже и останется истинным.
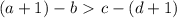
Соответственно увеличивали числа b и c:
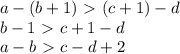
Действие аналогично прибавлению 2 к правой части и именно оно изменило истинность неравенства