1,225*100/1.25=98%
100%-98%=2%
Решение задачи автотуристы за три дня проехали 360 км.В первый день они проехали две пятых,а во второй день три восьмых
всего пути.Сколько км проехали авто туристы в третий день.
ответ или решение1
В начале найдём сколько км автотуристы проехали в первый день:
360 * 2/5 = 360 : 5 * 2 = 144 (км).
Во второй день туристы проехали:
360 * 3/8 = 360 : 8 * 3 = 135 (км).
Значит за два дня они проехали:
144 + 135 = 279 (км),
а за третий день проехали:
360 - 279 = 81 (км).
За два дня автотуристы проехали такую часть пути:
2/5 + 3/ 8 = (16 + 15)/40 = 31/40.
Значит в третий день им осталось проехать:
1 - 31/40 = 4/40 - 31/40 = 9/40 пути.
Таким образом в третий день они проехали:
360 * 9/40 = 360 : 40 * 9 = 81 (км).
Пошаговое объяснение:
Вот ответь и решение
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
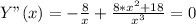
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении

1,225 - Х%
х=1,225*100:1,25=98%
100%-98%=2%