1)
14 2
7 7
1
14=7*2
26 2
13 13
1
26=13*2
35 5
7 7
1
35=7*5
38 2
19 19
1
38=2*19
52 2
26 2
13 13
1
52=2*2*13
87 3
29 29
1
87=29*3
2)
88 2
44 2
22 2
11 11
1
88=2*2*2*11
136 2
68 2
34 2
17 17
1
136=2*2*2*17
222 2
111 3
37 37
1
222=2*3*37
246 2
123 3
41 41
1
246=2*3*41
385 5
77 7
11 11
1
385=5*7*11
435 5
87 3
29 29
1
435=5*3*29
530 2
265 5
53 53
1
530=2*5*53
555 5
111 3
37 37
1
555=5*3*37
3)
396 2
198 2
99 3
33 3
11 11
1
396=2*2*3*3*11
456 2
228 2
114 2
57 3
19 19
1
456=2*2*2*3*19
504 2
252 2
126 2
63 3
21 3
7 7
1
504=2*2*2*3*3*7
700 2
350 2
175 5
35 5
7 7
1
700=2*2*5*5*7
594 2
297 3
99 3
33 3
11 11
1
594=2*3*3*3*11
1170 2
585 5
117 3
39 3
13 13
1
1170=2*5*3*3*13
2310 2
1155 5
231 3
77 7
11 11
1
2310=2*5*3*7*11
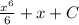
Пошаговое объяснение:
ну согласно свойствам интегралов, коих множество и изучить их надо, чтобы понимать и легко решать, данный интеграл можно представить следующим образом:

это уже сумма двух табличных интегралов.
Заглядываем в таблицу интегралов, которую Вы должны выучить наизусть как таблицу умножения и уже должна быть выучена наизусть таблица производных.
Это опять же, если Вы хотите легко и хорошо решать такие примеры.
В таблице находим похожий интеграл:
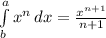
подставляем наши значения по аналогии в данный табличный пример и получаем:
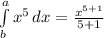
и со вторым выражением также:
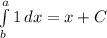
Вот и решили, осталось записать всё в одну строчку:
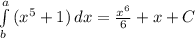
6a^2=1a
a=1/√6
V=a^3
v=1/6√6