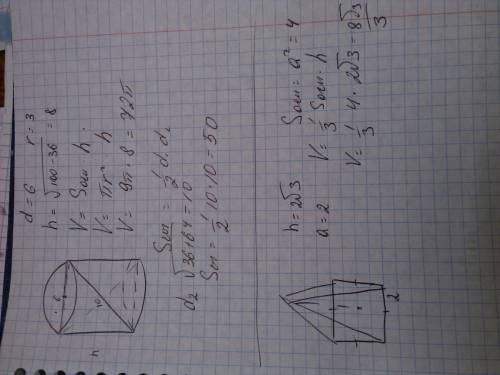
ответ:Биссектриса делит угол, из которого выходит, пополам. От сюда, можно узнать что углы ∠ABD и ∠DBC=80/2=40°
Рассмотрим треугольник ABD, в нем мы знаем два угла: ADB и ABD. Зная два угла в треугольнике можно найти третий угол, т. к. сумма углов в треугольнике равна 180°. Тогда: 180°-(40°+120°)=20°. Т. е. угол ∠DAB = 20°;
Теперь рассмотрим треугольник ABC, в нем мы теперь знаем два угла: ∠A (равен углу ∠DAB ) и угол ∠B, отсюда можно найти третий угол ∠C: 180°-(20°+80°)=80°.
Рассмотри треугольник DBC, в нем нам известны два угла ∠DBC и ∠C, найдем третий угол: 180°-(40°+80°)=60°.
ответ: В треугольнике CBD углы: ∠CBD=40°, ∠C=80°, ∠CDB=60°.
Sосн=πd²/4=π*6²/4=9π
Рассматривем прямоугольный треугольник в осевом сечении цилиндра, в котором основание - диаметр цилиндра, а гипотенуза - диагональ в осевом сечении, находим по теореме Пифагора высоту треугольника, которая также является высотой пирамиды. h=√(d1²-d²)=√(100-36)=√64=8
Площадь осевого сечения равна d*h=6*8=48 (ед.кв.)
Объем цилиндра V=Sосн*h=9π*8=72π (ед.куб.)
2. Объем пирамиды равен 1/3 * Sосн * h =1/3 * 2 * 2 * 2√3 = (8√3)/3