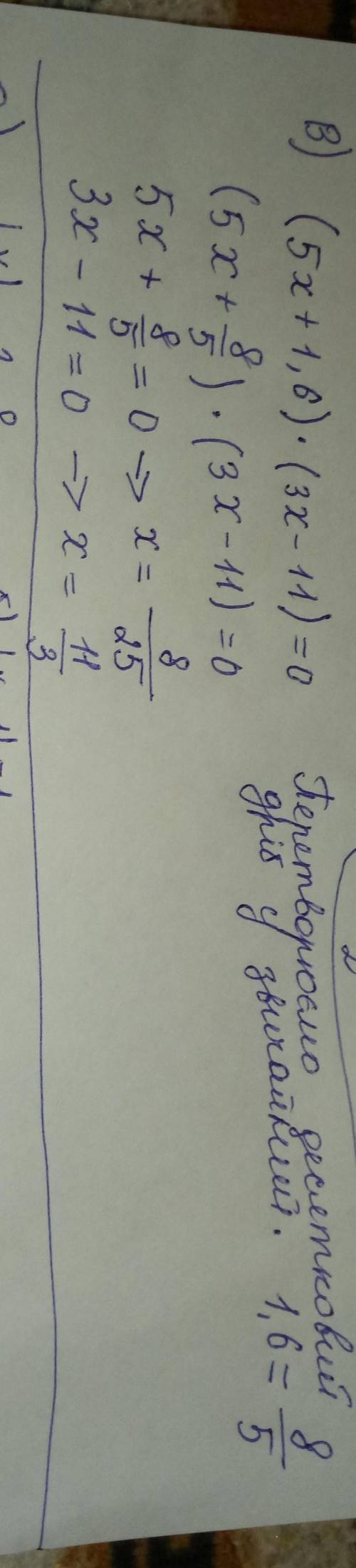ответ:Воспользуемся формулой Лапласа
вероятность, что событие наступит k раз при n испытаниях
P(k) = 1/корень (npq) * ф [ (k-np)/корень (npq) ], где
p - вероятность события, q = 1-p, ф - функция Гаусса
ф (x) = 1/корень (2pi) * e^(-x^2 / 2)
n = 1600, k = 1200, p = 0.8, q = 0.2
np = 1280, корень (npq) = 16
x = (k-np)/корень (npq) = -80 / 16 = -5
ф = 1/корень (2pi) * e^(-x^2 / 2) = 0.3989 * e^(-12.5) = 0,3989*3,731*10^(-6) = 1.488*10^(-6)
P(1200) = 1/16 * 1.488*10^(-6) = 0.93*10^(-7)
вероятность ничтожно мала - меньше одной десятимиллионной
Пошаговое объяснение:Воспользуемся формулой Лапласа
вероятность, что событие наступит k раз при n испытаниях
P(k) = 1/корень (npq) * ф [ (k-np)/корень (npq) ], где
p - вероятность события, q = 1-p, ф - функция Гаусса
ф (x) = 1/корень (2pi) * e^(-x^2 / 2)
n = 1600, k = 1200, p = 0.8, q = 0.2
np = 1280, корень (npq) = 16
x = (k-np)/корень (npq) = -80 / 16 = -5
ф = 1/корень (2pi) * e^(-x^2 / 2) = 0.3989 * e^(-12.5) = 0,3989*3,731*10^(-6) = 1.488*10^(-6)
P(1200) = 1/16 * 1.488*10^(-6) = 0.93*10^(-7)
вероятность ничтожно мала - меньше одной десятимиллионной
Відповідь: Буде на фото, якщо щось не зрозуміло, пишіть в коментарях.
1. а) х•(х-7)=0
х-7=0
х=0+7
х=7
б) на фото.
в) на фото.
2.
а) |х|=2,8
х= -2,8
х=2,8
б) |х-1|=1
х-1=1 Або х-1=-1
х=1+1 х=-1+1
х=2 х=0
в) |2х+3,6|=2,2
2х+3,6=2,2 або 2х+3,6=-2,2
2х=2,2-3,6 2х=-2,2-3,6
2х= -1,4 2х=-5,8
х= -1,4:2 х=-5,8:2
х= -0,7 х=-2,9
Потрібно переписувати два варіанти розв'язку, на слово або увагу не звертаємо, просто в математиці такі рівняння розв'язуються двома випадкам і пишеться слово або.
Якщо щось буде не зрозуміло, пишіть в коментарях.