при ![a \in ( - \infty ;\,\, - 8] \cup [ - 1;\,\, + \infty )\ x = 3;](/tpl/images/4978/6766/bd071.png)
при 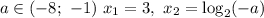
Пошаговое объяснение:
1) 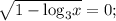
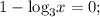
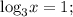

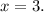
2) Данное уравнение равносильно такой совокупности:
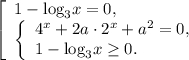
Первое уравнение было решено выше.
Рассмотрим систему
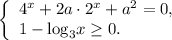
Уравнение системы — полный квадрат 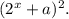 Поэтому
Поэтому
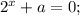
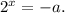
Так как функция 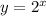 принимает только положительные значения при всех
принимает только положительные значения при всех 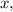 при
при 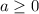 данное уравнение корней не имеет, а при
данное уравнение корней не имеет, а при 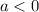
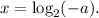
Решим неравенство системы:
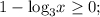
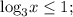
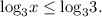
Так как функция 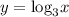 является возрастающей и учитывая ее область определения, получаем
является возрастающей и учитывая ее область определения, получаем 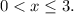
Таким образом число 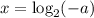 будет являться корнем исходного уравнения только тогда, когда будет удовлетворять неравенству
будет являться корнем исходного уравнения только тогда, когда будет удовлетворять неравенству 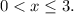
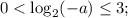
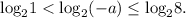
Так как функция 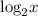 является возрастающей,
является возрастающей,
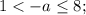
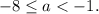
Выяснили, что данное уравнение всегда будет иметь корень 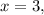 а корень
а корень 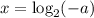 — только при
— только при 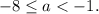
Отдельно можно выделить случай, когда оба эти корня совпадают:
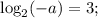
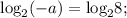
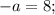
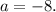
Итак,
при ![a \in ( - \infty ;\,\, - 8] \cup [ - 1;\,\, + \infty )](/tpl/images/4978/6766/43746.png)
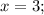
при 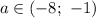
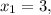
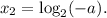
1; 3
Пошаговое объяснение:
Разобьем числовую прямую на три промежутка двумя точками, в которых модули обращаются в 0, т. е. точками 1 и 2, и рассмотрим данное уравнение на каждом из промежутков.
Сами точки 1 и 2 тоже следует включить по одному разу в какой-то из промежутков. В решении они обе включены во второй. Если включить их как-то иначе, на ответ задачи это не повлияет.
1) 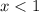
Тогда 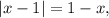
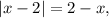 значит
значит
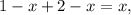
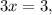
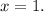
Найденное значение не находится в промежутке 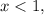 поэтому на этом промежутке уравнение решений не имеет.
поэтому на этом промежутке уравнение решений не имеет.
2) 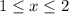
Тогда 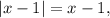
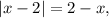 значит
значит
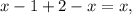
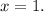
Найденное значение принадлежит промежутку 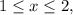 поэтому
поэтому 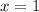 — корень.
— корень.
3) 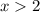
Тогда 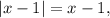
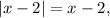 значит
значит
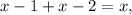
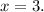
Найденное значение принадлежит промежутку 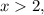 поэтому
поэтому 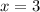 — корень.
— корень.
а) какое из двух чисел является делителем другого? В принципе они оба могут быть делителями другого. Но поскольку вряд ли это 17/3451= 0,0049261083743842 , то
17- делитель 3451, а 3451-делимое
Назовите ещё 3 делителя этого числа. 7, 29, 493
б) какое из двух чисел кратно другому числу? 3451 кратно 17
Назовите ещё три числа кратных этому числу 51, 170, 7786