![\lim\limits_{n\to\infty}n(\sqrt{n^2+2}-\sqrt{n^2-2})=\lim\limits_{n\to\infty}\frac{n(\sqrt{n^2+2}-\sqrt{n^2-2})(\sqrt{n^2+2}+\sqrt{n^2-2})}{\sqrt{n^2+2}+\sqrt{n^2-2}}\\\\=\lim\limits_{n\to\infty}\frac{n\left[(\sqrt{n^2+2})^2-(\sqrt{n^2-2})^2]}{\sqrt{n^2(1+\frac{2}{n^2})}+\sqrt{n^2(1-\frac{2}{n^2})}}=\lim\limits_{n\to\infty}\frac{n(n^2+2-n^2+2)}{n\sqrt{1+\frac{2}{n^2}}+n\sqrt{1-\frac{2}{n^2}}}](/tpl/images/0279/7172/fafec.png)
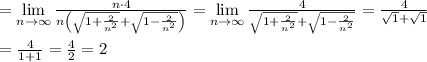
Формула для силы притяжении равна
F=(G*m1m2)/R2
Возьмём планету #1 как а, а планету #2 как б
a звезду как з
Тогда
F a=(G*m a* m з)/R2 a
F б=(G*m б* m з)/R2 б
Известно, что сила притяжения первой больше второй в 9 раз. значит F a=F б*9
А значит:
(G*m a* m з)/R2 a=9*(G*m б* m з)/R2 б
Далее. Массы планет а и б равны, значит уберем в формуле а и б и оставим просто m.
(G*m* m з)/R2 а=9*(G*m* m з)/R2 б
Далее G и m з одинакова поэтому сократим обе части на G и m з
m/R2 а=9*m/R2 б
массы планет равны. сократим на m
1/R2 а=9/R2 б
1/R a= 3/R б
3R a=R б
Формула для силы притяжении равна
F=(G*m1m2)/R2
Возьмём планету #1 как а, а планету #2 как б
a звезду как з
Тогда
F a=(G*m a* m з)/R2 a
F б=(G*m б* m з)/R2 б
Известно, что сила притяжения первой больше второй в 9 раз. значит F a=F б*9
А значит:
(G*m a* m з)/R2 a=9*(G*m б* m з)/R2 б
Далее. Массы планет а и б равны, значит уберем в формуле а и б и оставим просто m.
(G*m* m з)/R2 а=9*(G*m* m з)/R2 б
Далее G и m з одинакова поэтому сократим обе части на G и m з
m/R2 а=9*m/R2 б
массы планет равны. сократим на m
1/R2 а=9/R2 б
1/R a= 3/R б
3R a=R б