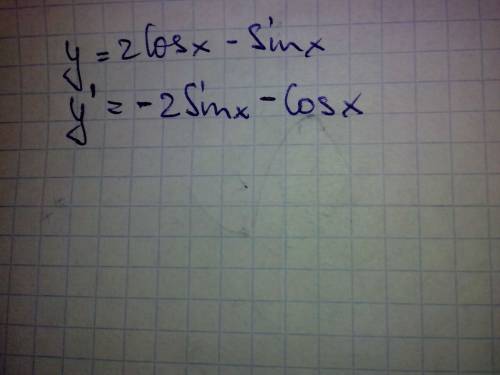
а) 1/12 и 1/35 = 35/420 и 12/420
12=2*2*3 35=5*7 НОК (12 и 35) = 12 * 35 = 420
420 : 12 = 35 - доп.множ. к 1/12 = (1*35)/(12*35) = 35/420
420 : 35 = 12 - доп.множ. к 1/35 = (1*12)(35*12) = 12/420
б) 17/96 и 41/72 = 51/288 и 164/288
96=2*2*2*2*2*3 72=2*2*2*3*3 НОК(96и72)=2*2*2*2*2*3*3=288
288 : 96 = 3 - доп.множ. к 17/96 = (17*3)/(96*3) = 51/288
288 : 72 = 4 - доп.множ. к 41/72 = (41*4)/(72*4) = 164/288
в) 5/56 и 17/29 = 145/1624 и 952/1624
56*29=1624 - наименьший общий знаменатель число)
1624 : 56 = 29 - доп.множ. к 5/56 = (5*29)/(56*29) = 145/1624
1624 : 29 = 56 - доп.множ. к 17/29 = (17*56)/(29*56) = 952/1624
г) 5/17 и 9/13 = 65/221 и 153/221
17*13=221-наименьший общий знаменатель (17и числа)
221 : 17 = 13 - доп.множ. к 5/17 = (5*13)/(17*13) = 65/221
221 : 13 = 17 - доп.множ. к 9/13 = (9*17)/(13*17) = 153/221
там ещё ест другие дроби
x1, x2, x3, x4, x5, x6, x7, x8 числа при вершинах
x1+x2, x2+x3, x3+x4, x4+x5, x5+x6, x6+x7, x7+x8, x1+x8 числа на сторонах
или запишем как
x1+x2=a1
x2+x3=a2
x3+x4=a3
x4+x5=a4
x5+x6=a5
x6+x7=a6
x7+x8=a7
x8+x1=a8
Отметим что если такие числа существует то должно выполнятся равенство
a1+a3+a5+a7=a2+4+a6+a8 (порядок в каком брать числа здесь не важен)
Проверим можно ли разбить 11,12,13,14,15,16,17,18 в нужную сумму, сложив числа 11+12+13+14+15+16+17+18=116 откуда 116/2=58 то есть такой порядок последовательности возможна, как пример
x1=2, x2=9, x3=3, x4=11, x5=2, x6=13, x7=3, x8=15