ДАНО:
V1 = 30 км/ч - скорость мопедов.
t1 = 10 мин - задержка на старте мопедов
t2 = 4 мин - задержка на встрече с мотоциклом
НАЙТИ: V2=? - скорость мотоциклиста.
Пошаговое объяснение:
t1 = 10 мин = 1/6 ч. и t2 = 4 мин = 1/15 ч. - другие единицы времени.
1) d = V1*t1 = 30 * 1/6 = 5 км - расстояние между мопедами.
2) Vc = V1 + V2 = 30 + V2 - скорость сближения.
3) Vc = d/t2 = 5/(1/15) = = 5*15 = 75 км/ч - скорость сближения.
4) V2 = Vc - V1 = 75 - 30 = 45 км/ч - скорость мотоцикла - ответ.
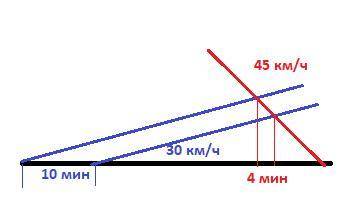
Схема-график встречного движения на рисунке в приложении.
ответ:
пусть о - центр вписанной окружности, n - точка касания окр со стороной ac, k - точка касания окр со стороной bc, m - точка касания окружности со стороной ab, тогда mb = x, am =2x (2/1 от a), значит ab =3x. по утверждению со стр.167 учебника - отрезки касательных к окружности , проведенные из одной точки равны и составляют ровные углы с прямой проходящей через эту точку и центр окружности - am =an, an =2x и bk =x. аналог. ck =cn =15-2x.(т.к. ac=15, a an =2x).периметр будет ab+bc+ac=3x+(x+15-2x)+(2x+15-2x)=42.решив уравнение имеем x=6. 3н. ab=18 см,ac=15 см, bc=9см
пошаговое объяснение:
54 (единица длины)
Пошаговое объяснение:
Скорость точки движения изменяется по закону
υ(t)=36·t-12·t².
Тогда из υ(t)=0 получаем t₀ - время начало движения и t₁ - время остановки:
36·t-12·t²=0 ⇔ 12·t·(3-t)=0 ⇔ t₀=0 и t₁=3.
Так как производная от пути S(t) равна скорости, то есть S'(t)=υ(t), определяем S(t) интегрированием:
S(t)=∫υ(t)dt=∫(36·t-12·t²)dt=36·t²/2 - 12·t³/3 + С=18·t² - 4·t³ + С.
В начале движения пройдённый путь равна нулю и поэтому:
S(t)=0 ⇔ 18·0² - 4·0³ + С = 0 ⇔ С=0.
Значит S(t)=18·t² - 4·t³. Тогда
S(3)=18·3² - 4·3³=18·9 - 4·27=162 - 108= 54 (единица длины).