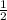 основания.
основания.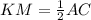
C древних времен домашние животные являются нашими спутниками. Считается, что первой была собака, она человеку охотиться и охраняла дом, а затем нашлось предназначение и другим животным. Постепенно люди привыкли, что рядом с ними находятся маленькие питомцы, и сейчас многие из нас не представляют без них своей жизни. Самыми популярными в наше время являются кошки, затем собаки, многие держат птиц и рыбок, грызуны и черепахи встречаются реже, а вот рептилии и насекомые - очень редкие питомцы. Тем не менее, трудно найти человека, который не любит животных, и зачастую мы убеждены, что знаем о них все, но оказывается, это не так.Даже ученые-биологи, проводя различные эксперименты и наблюдая за братьями меньшими, часто удивлены результатами. Собаки отличаются хорошим зрением, они видят неподвижные предметы на расстоянии до 500 м, а движущиеся - до 900 м, а их нюх поистине уникален: считается, что среди миллиарда бочек с хорошими яблоками собака сможет найти одно гнилое.
По свойству средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна её половине. Значит, средняя линия MN будет параллельна стороне BC и равна BC/2.
Следовательно, для определения длины средней линии треугольника достаточно знать длину стороны именно этой третьей стороны.2Пусть теперь известны стороны, середины которых соединяет средняя линия MN, то есть AB и AC, а также угол BAC между ними. Так как MN - средняя линия, то AM = AB/2, а AN = AC/2.
Тогда по теореме косинусов справедливо: MN^2 = (AM^2)+(AN^2)-2*AM*AN*cos(BAC) = (AB^2/4)+(AC^2/4)-AB*AC*cos(BAC)/2. Отсюда, MN = sqrt((AB^2/4)+(AC^2/4)-AB*AC*cos(BAC)/2).3Если известны стороны AB и AC, то среднюю линию MN можно найти, зная угол ABC или ACB. Пусть, например, известен угол ABC. Так как по свойству средней линии MN параллельна BC, то углы ABC и AMN - соответствующие, и, следовательно, ABC = AMN. Тогда по теореме косинусов: AN^2 = AC^2/4 = (AM^2)+(MN^2)-2*AM*MN*cos(AMN). Следовательно, сторону MN можно найти из квадратного уравнения (MN^2)-AB*MN*cos(ABC)-(AC^2/4) = 0.