- числитель исходной дроби, тогда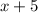 
- знаменатель этой же дроби. 
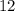получилась дробь, которая в 
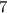раз больше исходной. Так как знаменатель остался прежним, то числитель второй дроби в 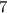раз больше числителя исходной дроби.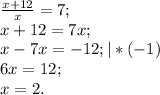
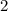- числитель исходной дроби.
.
.
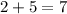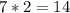∛(9-x) +∛63+x=6
Это уравнение можно свести к системе:
cделаем 2 замены:
∛(9-x)=a
∛(63+x)=b
Откуда можно записать систему
a+b=6
a^3+b^3=9-x+63+x=72
a^3+b^3=(a+b)(a^2-ab+b^2)
Деля 2 на 1 уравнение получим:
a^2+b^2-ab=72/6=12
выразив: a=6-b
(6-b)^2+b^2-b(6-b)=12
36-12b+b^2+b^2-6b+b^2=12
3b^2-18b+24=0
b^2-6b+8=0
По теореме виета:
b1=4
b2=2
То есть возможно 2 варианта:
∛(63+x)=4
63+x=64
x=1
2)∛(63+x)=2
63+x=8
x=-55
ответ:x=1 x=-55