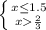
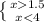
Пошаговое объяснение:
есть чудесный метод , называется метод неопределенных коэффициентов
но мне лень и я решил те же коэффициенты подсчитать по другому
5/((x-2)(x+4)(x+6)) = A/(x-2)+B/(x+4)+C/(x+6)
поднимите руку кому не лениво вычислять А В С в лоб.
вижу что негусто, поэтому схитрю
при х->2 выражение сильно стремится к бесконечности и ведет себя как
5/((x-2)(x+4)(x+6)) = 5/((x-2)(2+4)(2+6))=5/48 * 1/(x-2)
Вы заметили что мы только что вычислили А ???
при х->-4 выражение сильно стремится к бесконечности и ведет себя как
5/((x-2)(x+4)(x+6)) = 5/((-4-2)(х+4)(-4+6))=-5/12 * 1/(х+4)
при х->-6 выражение сильно стремится к бесконечности и ведет себя как
5/((x-2)(x+4)(x+6)) = 5/((-6-2)(-6+4)(x+6))=5/16 * 1/(x+6)
конечный оtвет
5/48*ln(|x-2|) - 5/12*ln(|х+4|) + 5/16 *ln(|x+6|) + const
т.е. решением является промежуток (2/3;4), а число целых решений на отрезке [0;4] получается 3: это 1, 2, 3