х = 0
Объяснение:
(5х · (-8)) · 2 - (4х · (-3)) · 2 + 26х = 0
(перемножаем всё, что находится в скобках)
-30х · 2 - (-12)х · 2 + 26х = 0
(при умножении положительного числа на отрицательного ответ будет отрицательный - со знаком "-")
-60х - (-24)х + 26х = 0
(минус на минус даёт нам плюс)
-60х + 24х + 26х = 0
(для удобства поменяем местами слагаемые)
26х + 24х -60х = 0
(50 - 60 = -10)
-10х = 0
(при переносе через знак "=" меняем знак)
х = 0 : 10
(при делении на нуля на любое число, не равное нулю, получим нуль)
х = 0
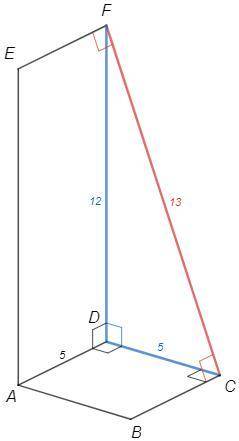
Угол между плоскостями - угол между перпендикулярами к линии пересечения плоскостей.
∠FDA=90, ∠CDA=90 => ∠FDC - линейный угол двугранного угла FADC.
Плоскости перпендикулярны, угол между ними - прямой, ∠FDC=90
Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна плоскости, FD⊥(ABC).
FD⊥(ABC), DC⊥BC => FC⊥BC (по теореме о трех перпендикулярах)
Аналогично FC⊥EF
Расстояние между прямыми - длина общего перпендикуляра.
FC - искомое расстояние
AD =CD =√S(ABCD) =√25 =5
FD =S(AEFD)/AD =60/5 =12
FC =√(CD^2 +FD^2) =13 (см) (т Пифагора)
abc - трёхзначное число
a + b + c = 11
a^2 + b^2 + c^2 = 69
___ ___
abc + 693 = cba
100а + 10b + c + 693 = 100c + 10b + a
99c - 99a = 693
99(c - a) = 693
c - a = 7
c = 7 + a
b + a + 7 + a = 11
b + 2a = 4
b = 4 - 2a
a^2 + (4 - 2a)^2 + (7 + a)^2 = 69
a^2 + 4a^2 +a^2 -16a + 14a + 16 + 49 = 69
6a^2 - 2a - 4 = 0
3a^2 - a - 2 = 0
D = 1+ 24 = 25
a = (1 + 5)/2*3 = 1
b = 4 - 2*1 = 4 - 2 = 2
c = 7+1 = 8
128 - трёхзначное число