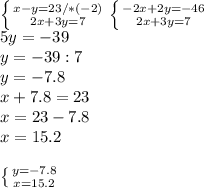
ответ:6 и 18 см.
Пошаговое объяснение:Составляем уравнение, в котором ширину прямоугольника записываем как х см.
Поскольку его длина на 12 см больше, она будет равна: х + 12 см.
Поскольку площадь прямоугольника является произведением его сторон, получим следующее выражение:
х * (х + 12) = 108.
х^2 + 12 * х = 108.
Получаем квадратное уравнение:
х^2 + 12 * х - 108 = 0.
Д^2 = (12)^2 - 4 * 1 * (-108) = 144 + 432 = 576.
Д = √576 = 24.
х = (-12 + 24) / 2 = 12 / 2 = 6 см (ширина прямоугольника).
х + 12 = 6 + 12 = 18 см (длина).
6 и 18 см.
ну, в первой загадке вы опечатались в условии, похоже:
должно быть так: "через точку а к окружности w (0,r)проведены". а то выходит, что а принадлежит окружности, при этом через нее аж две касательные
ну а доказывать, полагаю, надо через равенство треугольников, образующихся при соединении этой точки а с центром окружности и радиусов, проведенных к точкам касания в и с.
треугольники аво и асо:
во-первых, прямоугольные. (углы в и с прямые, ибо радиус к точке касания перперндикулярен касательной);
во-вторых, имеют равные катеты ов и ос (длина их - радиус окружности);
в-третьих - у них равные гипотенузы (она у них общая, это отрезок ао);
значит они равны (по углу и двум сторонам)
следовательно ав=ас.
согласны?
а вот что думаю про вторую :
раз угол прямой, то, соединив отрезками точки касания с центром окружности, получим симпатичный квадрат, диагональ которого - та самая хорда.
ну, а у квадрата диагонали равны и перпендикулярны друг другую.
значит проводим вторую диагональ (она как раз из центра к хорде под прямым углом пойдет) и сразу становится видно, что расстояние от хорды то центра окружности окружности - ровно половина диагонали, т.е.
40/2 = 20см
ура?
))
2х+3у=7 2(23+y)+3y=7 46+2y+3y=7 46+5y=7
x=23+y x=23+y x=23+y x=23+y x=23+(-7,8) x=15,2
5y=7- 46 5y=-39 y=-39:5 y=-7,8 y=-7,8 y=-7,8