Объяснение: Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого. Или, что даст ту же длину:
чтобы найти длину отрезка на координатной прямой, надо из координаты одного конца вычесть координату другого конца.
ответ будет равен модулю полученного результата:
* * *
По определению серединой отрезка АВ называется точка С, если она лежит на отрезке АВ и находится на одинаковом расстоянии от его концов. Если точка С – середина отрезка АВ, то |АС|=|СВ|.
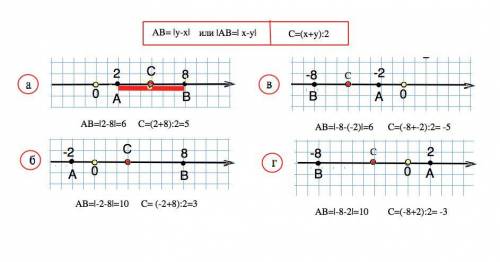
Координата середины отрезка равна полусумме координат концов отрезка: (Ах+Ву): 2.
а) С=(2+8):2=5
б) С=(-2+8):2=3
в) С=(-8+-2):2=-5
г) С=(-8+2):2=-3
ответ:Пусть в классе х учеников. Если Вовочка исправит двойки, то двоечников будет – 0,24х. Если его выгонят, то двоечников будет 0,25(х – 1).
1) Составим уравнение:
0,25(х – 1) = 0,24х
х = 25
Значит, в классе 25 учеников.
2) 0,25 . (25 – 1) = 6 (учеников) – двоечников в классе
3) 6+1 = 7 (учеников) – двоечников вместе с Вовочкой сейчас
4) 7 : 25 . 100=28 (%) - двоечников вместе с Вовочкой сейчас
ответ: 28% двоечников в своем классе
Пошаговое объяснение:
удачи
кто хочет подружиться со мной кидайте я приму
Поскольку задача указана для средней школы, то решим задачу в лоб, что длиннее.
Для начала нужно выкинуть cos из уравнения, чтобы можно было заменой уйти от тригонометрических функций.
=
=>
=>
В случае, если
=> При
То есть при
Поскольку z - это корень, то по определению корня это неотрицательное число =>
=>
=>
=>
При этом должно выполняться неравенство
Решения есть, если
=>
=>
=>
=>
Поскольку мы ищем наименьший корень, то что числитель должен быть наименьшим при минимальном k либо максимальным при минимальном k, найденные числа необходимо сравнить => Найдём сначала наименьшее значение
Выражение
=> Выражение
=> Выражение
Это формула параболы с ветвями, направленными вниз с вершиной при k=1. При этом вспомним, что в выражении (1*) мы требуем, чтобы данное выражение было
=> Наименьших значений это выражение будет достигать в точках пересечения с 0
=>
=>
Поскольку у нас ограничения для
Проверим это значение U ещё вот по этому ограничению :
=>
=> k=1 =>
Вообще, нужно ещё доказать, что минимальное значение арксинуса в сумме с слагаемым при k=1 меньше, чем максимальное значение арксинуса при k=0.
Арксинус максимален в вершине параболы описывающей его числетель => U=1 =>
=>
=>
Теперь определим, которое из чисел меньше. Вычтем из x (11) 2:
=
/Для упрощения оценки допустим, что арксинус достигает своего максимального значения =
=
Следовательно x=2 - это минимальный корень из всех возможных.
ответ: x=2
Просто кошмар, это решение стоит намного больше, чем
Прилагаю график, на котором изображена функция tex]sin \frac{ \pi x}{4} + cos \frac{ \pi x}{4}[/tex], а также y=x, которая служит ограничением по условиям задачи