Пусть a, b, c - первые три члена арифметической прогрессии, тогда по условию:
а + b + с = 15 [1]
По свойству арифметической прогрессии:
b - а = с - b
2b = а + с подставим в уравнение [1], получим:
2b + b = 15
3b = 15
b = 5 - второй член арифметической прогрессии.
Тогда сумма первого и третьего членов:
а + с = 15 - 5
а + с = 10 ⇒ c = 10 - a
Переходим к геометрической прогрессии. По условию:
первый член = а + 1
второй член = b + 3 = 5 + 3 = 8
третий член = с + 9 = 10 - a + 9 = 19 - a
По свойству геометрической прогрессии:

 не удовл.условию, так как искомая геометрическая прогрессия возрастающая.
не удовл.условию, так как искомая геометрическая прогрессия возрастающая.
Получили а = 3, тогда с = 10 - а = 10 - 3 = 7
Итак, первые три члена арифметической прогрессии: 3; 5; 7.
Найдем три первых члена геометрической прогрессии:
первый член = а + 1 = 3 + 1 = 4
второй член = 8
третий член = с + 9 = 7 + 9 = 16
Искомая геометрическая прогрессия: 4; 8; 16; ...
Найдем сумму 7 первых членов.
b₁ = 4 - первый член
q = b₂/b₁ = 8/4 = 2 - знаменатель прогрессии
Искомая сумма:

ответ: 508
a=-6
Пошаговое объяснение:
(|x|-2)(|x|-4)=2-a
(|x|-2)(|x|-4)-2+a=0
рассмотрим функцию f(x)=(|x|-2)(|x|-4)-2+a
Она непрерывна на всей числовой оси.
f(-x)=(|-x|-2)(|-x|-4)-2+a=(|x|-2)(|x|-4)-2+a=f(x) ⇒ функция четная.
Если четная функция имеет НЕчетное количество корней, то один из них обязательно будет 0.
для уравнения: (|x|-2)(|x|-4)=2-a, при х=0, получаем
(0-2)(0-4)=2-a
-2*(-4)=2-a
8=2-a
a=2-8
a=-6 - при таком значении a уравнение имеет нечетное число различных корней.
Проверим, будет ли их ровно 3:
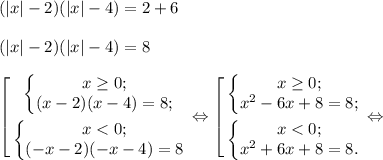
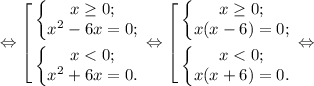
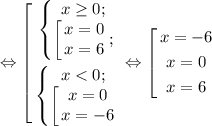
Действительно, при a=-6 получилось 3 корня!
ответ: a=-6
1,5/60*100=1,5/6*10=0,5/2*10=0,5*5=2,5кг-вес нового сплава
2,5-2=0,5кг- надо добавить цинка