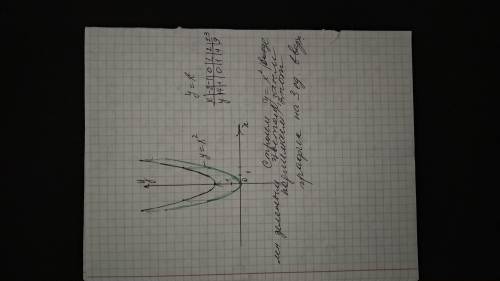
1. Область определения х∈(-∞;+∞)
2. Множество значений у∈[3;+∞)
3. нулей нет. т.к. парабола у= х²поднята на 3 ед. вверх. ветви ее направлены вверх.
при любых значениях х у больше нуля.
4. функция возрастает при х∈[0;+∞) и убывает при х∈(-∞;0)
5. функция четна. т.к. ее график симметричен относительно оси оу.
6. ограничена снизу.
7. нет . не обратима. х²=у-3; х=±√(у-3), у=±√(х-3); но если рассматривать данную функцию только на множестве положительных чисел, она будет обратимой, а вообще обратимая - это функция, у которой произвольному ее значению соответствует единственное значение аргумента.
график во вложении
1) Область определения?
2) Множество значений?
3) нули функции?
4) На каких интервалах функция убывает и возрастает?
5) Функция четная или нет?
6) Ограничена?
7) Обратима или нет?
1) 1,29
2) 20%
3) 18
4) Больше яблок ушло на компот, на 0,165 кг
5) Данных нет
6) 12,5%
7) В мешке было 10 кг муки
8) Искомое число - 25
Пошаговое объяснение:
1) 64,5*0,02=1,29
2) 0,8/4*100=20(%)
3) 4,5/0,25=18
4) 4.1) 10*0,05=0,5(кг)-для пирога
4.2) 10-0,5=9,5(кг)-осталось
4.3) 9,5*0,07=0,665(кг)-для компота
4.4) 0,665-0,5=0,165(кг)-разница
5) Для ответа на вопрос не хватает данных
6) 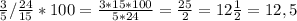 (%)
(%)
7) 7.1) 100-5=95(%)-осталось сначала
7.2) 8+1,5=9,5(кг)-осталось сначала
7.3) 9,5/0,95=10(кг)-было в мешке
8) Пусть число-x; тогда
x-0.5x*8=100
x/2*8=100
4x=100
x=100/4
x=25-исходное число
....просто в 10—13 вв. арабы.... в своих сочинениях принесли в Европу зту форму записи чисел... .
....отсюда и название!
Впервые эту индийскую систему записи использовал в 8 - 9 веке арабский учёный Мухаммед ибн Муса аль-Хорезми, автор знаменитой Китаб аль-Джебр ва-ль-Мукабаля, от названия которой произошёл термин «алгебра» .
Он.... упростил и обосновал систему начертания цифр.
Для обозначения 1,2,3, 4 ...он ввел соответствующее количество углов. В этих угловатых цифрах можно уже узнать знакомые нам цифири, четверка, например, обозначалась крестом. Символы же для остальных цифр были разработаны на основе абаки (счет) . 5 обозначалась кружочком под чертой, 6 и 7 - кружок под чертой и знаки для 1 или двух, пририсованные сверху. 10 обозначалось кружком над чертой, а для 8 и 9 снизу пририсовывались знаки для 2 и 1 (т. е. 8 - это 10 - 2). Соответственно, 10 в этом написании выглядело, как современное 10, перевернутое на 90 градусов против часовой стрелки.
Позднее, из десятки родился символ для нуля. На письме угловатости знаков слегка скруглялись, появлялись дополнительные черточки, другие же черточки исчезали.
В таком виде цифры попали в Европу.
В старинных европейских манускрипатах цифры отличались от привычных нам, постепенно цифра эволюционировали в знакомые всем символы. Во многих странах предпочтение отдавалось греческой и римской системам.
Распространились арабские цифры в Европе благодаря математику Леонардо Фибоначчи и итальянским купцам. Математик ознакомил итальянцев с индийско-арабской нумерацией, а итальянские купцы распространили эту систему по всей Европе