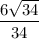
Пошаговое объяснение:
Синус острого угла прямоугольного треугольника - это отношение противолежащего (этому углу) катета к гипотенузе.
Если ∠A = 90° (по условию), то AB и AC - катеты данного треугольника. А BC - гипотенуза.
Противолежащим углу C катетом является AB.
В таком случае sinC = AB/BC. Но чтобы рассчитать синус угла, нужно знать длину гипотенузы.
Если даны длины любых двух сторон прямоугольного треугольника, то длину третьей можно вычислить по теореме Пифагора.
Теорема Пифагора:
Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.
По условию задачи известно, что AC = 14, AB = 12, тогда по теореме Пифагора:
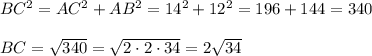
Теперь можем рассчитать sinC:
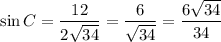
у = 1/3
в); г) 3/8 : 5/2 = у : 20/9
Пошаговое объяснение:
Дано:
у = 3/8 * 2 2/9 : 2 1/2
у = 3/8 * 20/9 : 5/2
у = 5/6 * 2/5
у = 1/3
В правильной пропорции произведение крайних членов пропорции равно произведению её средних членов и наоборот.
у = 3/8 * 2 2/9 : 2 1/2 где у - средний член пропорции, 3/8 и 2 2/9 - крайние члены пропорции и 2 1/2 - известный средний член пропорции, т.е.:
2 1/2 * у = 3/8 * 2 2/9 - произведение средних членов = произведению крайних членов
Составим и решим пропорцию:
3/8 : 2 1/2 = у : 2 2/9
3/8 : 5/2 = у : 20/9
3/8 : 5/2 = 1/3 : 20/9
3/8 * 2/5 = 1/3 * 9/20
3/20 = 3/20 - верно