130; 80; 160
Пошаговое объяснение:
1.угол D(вписанный), равный 50 градусам, опирается на дугу AВC. значит дуга АВС равна 100 градусам. дуга АDС равна 260 градусов, так как вся окружность 360 градусов. угол В(вписанный) опирается на дугу ADC, значит равен её половине, то есть 130 градусам.
2. угол ABD(вписанный), равный 40 градусам, опирается на дугу AD. значит дуга AD 80 градусов. угол AOD(центральный) равен дуге AD, на которую он опирается, то есть равен 80 градусам.
3. угол С(вписанный), равный 100 градусам, опирается на дугу АВ. значит дуга АВ равна 200 градусам. Соответственно, дуга АСВ 160 градусам. Искомый угол(центральный) опирается на дугу АСВ и равен 160 градусам.
Пошаговое объяснение:
1) ООФ
здесь знаменатель всегда ≠ 0, поэтому ООФ - вся числовая ось
2) функция не тригонометрическая
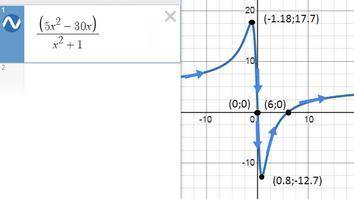
3) пересечение с осью оу (х = 0)
у(0) = 0 точка (0;0)
с осью ох (у=0)
из дроби приравниваем к 0 числитель
5х² -30х = 5х(х -6) ⇒
х₁ = 0 точка (0;0)
х₂ = 6 точка (6;0)
4) критические точки
для нахождения производной используем
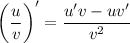
тогда
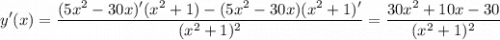
y'(x) = 0
10(3x² +x-3) = 0 ⇒ (значения определяем с точностью до 0,01)
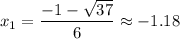
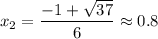
y(x₁) ≈ 17.707 точка (-1,18; 17,7)
у(х₂) ≈ -12,7 точка (0,8; -12,7)
5) промежутки возрастания и убывания. экстремумы
локальные экстремумы
у(≈-1,18) ≈ 17,7 - локальный максимум
у(≈0,8) ≈ -12,7 - локальный минимум
промежутки монотонности
(-∞ ;-1.18) f'(x) > 0 функция возрастает
(-1.18; 0.8) f'(x) < 0 функция убывает
(0.8; +∞) f'(x) > 0 функция возрастает
6)
6) поскольку промежуток ООФ, то концы промежутка (-∞; +∞)
при х → -∞ f(x) f(x) → -∞
при х → +∞ f(x) f(x) → +∞
7)
точки (0;0) (6;0)
(-1,18; 17,7) - локальный максимум
(0,8; -12,7) - локальный минимум
промежутки монотонности
(-∞ ;-1.18) f'(x) > 0 функция возрастает
(-1.18; 0.8) f'(x) < 0 функция убывает
(0.8; +∞) f'(x) > 0 функция возрастает
график прилагается
ответ: 2 яблока осталось.