√26sin(α+π/2), если ctgα=-5 , 0°<α<180°. Не могу понять как выбрать знак при косинусе ведь он лежит между 180 и 0
Пошаговое объяснение:
{ctgα=-5 ( котангенс отрицателен во 2и 4 четвертях)
{ 0°<α<180° ( это 1 и 2 четверти)
Из этих двух условий следует , что α∈ II четверти. Во 2 четверти cosα<0.
√26sin(α+π/2)= √26cosα
Т.к 1+ctg²α=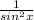
, то 1+(-5)²=
, sin²α=1/26.
По основному тригонометрическому тождеству
sin²α+cos²α=1
1/26+cos²α=1
cos²α=1-1/26
cos²α=25/26
cosα= -√(25/26) , cosα= -5/√26.
√26sin(α+π/2)= √26cosα= √26*(-5/√26)= -5
А) f(x) = 2х9 + 5х4 – 3х – 3;
Находим пресечение x, f (x) =0 и вычисляем сумму/разность:
0=18+20-3x-3;
0=35-3x;
3x=35;
x=11,6 или 35/3
ответ: 11,6 или 35/3
б) g(x)=2/х√х - перепишете заново непонятно, что и как вычислять.
в) q(x) = (4х+2)/3х
Находим пересечение с осью x, q (x)=0:
0=4x+2/3(дробь)*x
Рассматриваем оба варианта:
4x+2/3=0
или
x=0
x=-0,5
ответ: 0,5; 0.
г) u(x) = -cos х/8.
Находим пересечение с осью x, u (x)=0:
0=-cos x/8
-cos(x/8)=0
cos(x/8)=0
x/8=п(ПИ)/2+kп, а k лежит на(перевёрнутая э) Z
x=4п+8kп, k лежит на Z
Пошаговое объяснение:
