ответ
Пошаговое объяснение:
Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:
Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.
Случайные величины, как правило, обозначают через *, а их значения – соответствующими маленькими буквами с подстрочными индексами, например, .
* Иногда используют , а также греческие буквы
Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:
– количество очков, которое выпадет после броска игрального кубика.
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина может принять одно из следующий значений:
.
Пример из статьи о Статистическом определении вероятности:
– количество мальчиков среди 10 новорождённых.
Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:
, либо мальчиков – один и только один из перечисленных вариантов.
И, дабы соблюсти форму, немного физкультуры:
– дальность прыжка в длину (в некоторых единицах).
Её не в состоянии предугадать даже мастер спорта :)
Тем не менее, ваши гипотезы?
Коль скоро речь идёт о множестве действительных чисел, то случайная величина может принять несчётно много значений из некоторого числового промежутка. И в этом состоит её принципиальное отличие от предыдущих примеров.
Таким образом, случайные величины целесообразно разделить на 2 большие группы:
1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.
…нарисовались непонятные термины повторяем основы алгебры!
2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.
Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ
Сначала разберём дискретную случайную величину, затем – непрерывную.
Поехали:
1) Рассмотрим 2 случая
а) 
тогда уравнение принимает вид
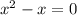

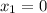
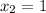
Оба корня удовлетворяют условию 1.
б) 
тогда уравнение принимает вид
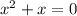
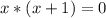
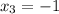
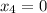
Последний корень не удовлетворяет 2-му условию. Значит он не является ответом.
ответ: 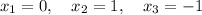
2) Снова рассматриваем 2 случая

тогда уравнение принимает вид
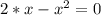
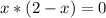

Оба корня удовлетворяют 1-му условию
б) 
тогда уравнение принимает вид
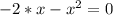
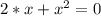
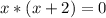
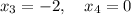
Последний корень не удовлетворяет 2-му условию. Значит он не является ответом.
ответ: 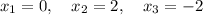
2x≥0, x≥0;
x²-8=0, (x-√8)(x+√8)=0,
x+2√2=0, x=-2√2,
x-2√2=0, x=2√2;
0≤x≤2√2, x²-8≤0,
-(x²-8)≤2x, x²-8≥-2x, x²+2x-8≥0,
x²+2x-8=0, D/4=1+8=9, x₁=-1-3=-4, x₂=-1+3=2,
x≤-4, x≥2;
2≤x≤2√2;
x≥2√2, x²-8≥0,
x²-8≤2x, x²-2x-8≤0,
x²-2x-8=0, D/4=1+8=9, x₁=1-3=-2, x₂=1+3=4,
-2≤x≤4;
2√2≤x≤4;
2≤x≤4, x∈(2;4).