Математика: Убоба было 5 конфет,он сьел 3. сколько конфет осталось?

Убоба было 5 конфет,он сьел 3. сколько конфет осталось?

👇

Увидеть ответ

Ответ:

sooooooyeees

02.06.2021

Пошаговое объяснение:

5-3=2конфеты

2 конфеты осталось

4,8(88 оценок)

Открыть все ответы

Ответ:

лиза2630

02.06.2021

Первоначально в бригаде было x рабочих, которые работали по y часов в день.

Производительность всей бригады 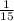$\frac1{15}$ всей работы в день или $\frac1{15y}$ всей работы в час.

Производительность одного рабочего 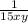$\frac1{15xy}$ всей работы в час.

Если бригадир наймет девять дополнительных рабочих, и при этом в день бригада будет работать на 2 часа меньше, то работа будет выполнена за 12 дней, то есть

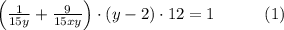
$\left(\frac1{15y}+\frac9{15xy}\right)\cdot(y-2)\cdot12=1\quad\quad\quad(1)$

Если бригадир уволит пятерых рабочих из первоначального состава бригады, то, чтобы окончить работу за 20 дней, бригаде придётся трудиться на 2 часа в день больше, то есть

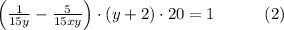
$\left(\frac1{15y}-\frac5{15xy}\right)\cdot(y+2)\cdot20=1\quad\quad\quad(2)$

Составим и решим систему уравнений (1) и (2):

$\begin{cases}\left(\frac1{15y}+\frac9{15xy}\right)\cdot(y-2)\cdot12=1\\\\\left(\frac1{15y}-\frac5{15xy}\right)\cdot(y+2)\cdot20=1\end{cases}\Rightarrow\begin{cases}\left(\frac1{15y}+\frac9{15xy}\right)\cdot(12y-24)=1\\\\\left(\frac1{15y}-\frac5{15xy}\right)\cdot(20y+40)=1\end{cases}\Rightarrow$

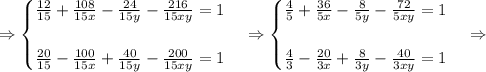
$\Rightarrow\begin{cases}\frac{12}{15}+\frac{108}{15x}-\frac{24}{15y}-\frac{216}{15xy}=1\\\\\frac{20}{15}-\frac{100}{15x}+\frac{40}{15y}-\frac{200}{15xy}=1\end{cases}\Rightarrow\begin{cases}\frac45+\frac{36}{5x}-\frac{8}{5y}-\frac{72}{5xy}=1\\\\\frac43-\frac{20}{3x}+\frac8{3y}-\frac{40}{3xy}=1\end{cases}\Rightarrow$

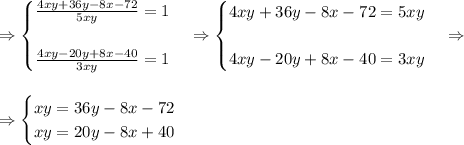
$\Rightarrow\begin{cases}\frac{4xy+36y-8x-72}{5xy}{}=1\\\\\frac{4xy-20y+8x-40}{3xy}=1\end{cases}\Rightarrow\begin{cases}4xy+36y-8x-72=5xy\\\\4xy-20y+8x-40=3xy\end{cases}\Rightarrow\\\\\\\Rightarrow\begin{cases}xy=36y-8x-72\\xy=20y-8x+40\end{cases}$

Вычтём из первого уравнения второе:

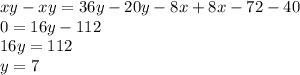
$xy-xy=36y-20y-8x+8x-72-40\\0=16y-112\\16y=112\\y=7$

Подставим значение y в любое из двух уравнений систему (например, во второе) и вычислим x:

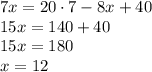
$7x=20\cdot7-8x+40\\15x=140+40\\15x=180\\x=12$

Тогда

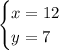
$\begin{cases}x=12\\y=7\end{cases}$

ответ: первоначально в бригаде было 12 рабочих, которые работали по 7 часов в день.

4,4(75 оценок)

Ответ:

школьник812

02.06.2021

Пошаговое объяснение:

цифры дадут 9999 варианто + 1 вариант (0000), т. е. 10000 вариантов.

Теперь разберемся с 32 буквами. Представим их трехзначные сочетания, как число, записанное в 32 ричной системе, где А соответствует цифре 0, а Я соответствует цифре 31 (да, да в 32-ричной системе может есть цифра 31!)

Тогда максимальное число из трех цифр в этой системе будет записано как ЯЯЯ.

Переведем это число в привычную нам десятичную систему счисления:

ЯЯЯ(32) = 31×32² + 31×32¹+31 = 31×(32²+32+1)=32767. По аналогии с 4 цифрами прибавим еще один вариант (ААА), соответствующий нулю в этой системе и получим, сочетание из 3-х букв 32 буквенного алфавита дает нам 32767+1=32768 вариантов. Каждому этому варианту может соответствовать любой из 10000 вариантов из 4 цифр. Поэтому для нахождения общего количества возможных вариантов их надо перемножить:

32768×10000=327680000 возможных вариантов номеров

Введем два события:

А: выбор вопроса по теме «Вписанная окружность»;

B: выбор вопроса по теме «Параллелограмм».

Так как нет вопросов, относящихся одновременно к этим двум темам, то события A и B несовместные. Вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем – это сумма вероятности событий A и B, имеем:

ответ: 0,35.

Т.к. 0,3*0,3 ≠ 0,12, то события "кофе закончится в первом автомате" и "кофе закончится во втором автомате" совместны (т.е. зависимы).

Обозначим событие А = "кофе останется в первом автомате", событие В = "кофе останется во втором автомате". Р(А)=Р(В)= 1-0,3=0,7.

Событие "кофе остался хотя бы в одном автомате" - это объединение событий А U B -событие, противоположное событию "кофе закончится в обоих автоматах).

Р(АUB) = 1-0,12=0,88

С другой стороны " кофе остался хотя бы в одном автомате" означает, что кофе остался или в первом или во втором или в обоих вместе .

Т.е. AUB = AUB U A∩B , тогда Р(AUB) = Р(А) + Р(B) - Р(A∩B)

Р(A∩B) = Р(А) + Р(B) - Р(AUB) = 0,7+0,7 - 0,88 = 0,52

ответ: 0,52

Общаться в чате

1) сдаст оба 0,7*0,3=0,21

2) не сдаст ни одного =такая же вероятность 0,3*0,7=0,21

3)сдаст хотя бы один — это противоположное событию, не сдаст не одного: р(А)=1-0,21=0,79

Поскольку в условии задачи не менее 2 вопросов, то задача распадается на две:

1) студенту попадётся билет с 3-мя вопросами, которые он знает;

2) студенту попадётся билет с 2-мя вопросами, которые он знает.