1) Рассмотрим треугольник АСД - прямоугольный (<АСД=90).
Т.к. <СДА=45, то по теореме о сумме углов треугольника <CАД=45. Следовательно, треугольник АСД - равнобедренный с основанием АД, а значит АС=СД.
2) <ВСА=<САД=45 (внутренние накрест лежащие углы при параллельных прямых АД и ВС - основания трапеции и секущей АС).
3) Рассмотрим треугольник АВС - прямоугольный (<АВС=90).
Т.к. <ВСА=45, то по теореме о сумме углов треугольника <САВ=45, т.е. треугольник АВС - равнобедренный с основанием АС, а значит АВ=ВС=5 см.
По теореме Пифагора
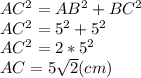
4) Из треугольника АСД по теореме Пифагора найдем АД:
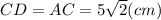
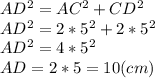
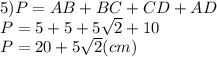
6) Трапеция АВСД - прямоугольная. АВ - высота трапеции, а значит
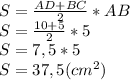
ответ: 20+5√2; 37,5
a)f(x)=(8x⁵-5x⁸)¹²
f ' (x) = ((8x⁵-5x⁸)¹²) ' = 12*(8x⁵-5x⁸)¹¹ * (8x⁵-5x⁸) ' = 12*(8x⁵-5x⁸)¹¹ * (40x⁴-40x⁷) = 12*(8x⁵-5x⁸)¹¹ * 40x⁴(1-x³) = 480x⁴ * (8x⁵-5x⁸)¹¹ * (1-x³)
б)f(X)=(1/9 - 3x³)²⁷
f ' (x) = ((1/9 - 3x³)²⁷) ' = 27(1/9 - 3x³)²⁶ * (1/9 - 3x³) ' = 27(1/9 - 3x³)²⁶ * (-3*3x²) = 27(1/9 - 3x³)²⁶ * (-9x²) = -243x² * (1/9 - 3x³)²⁶
в) f(x)=(4x¹⁰-5x)¹⁰
f ' (x) = ((4x¹⁰-5x)¹⁰) ' = 10(4x¹⁰-5x)⁹ * (4x¹⁰-5x) ' = 10(4x¹⁰-5x)⁹ * (40x⁹-5)= 10(4x¹⁰-5x)⁹ * 5(8x⁹-1)=50(4x¹⁰-5x)⁹ * (8x⁹-1)
г)f(x)=(x⁵-4x⁴)¹³⁰
f ' (x) = ((x⁵-4x⁴)¹³⁰) ' = 130(x⁵-4x⁴)¹²⁹ * (x⁵-4x⁴) ' = 130(x⁵-4x⁴)¹²⁹ * (5x⁴-16x³) = 130(x⁵-4x⁴)¹²⁹ * x³(5x-16) = 130*x³ * (x⁵-4x⁴)¹²⁹ * (5x-16)