Дана функция f(x)=4x³+x²-2x-6.
Её производная равна: y' = 12x²+2x-2.
Приравняем производную нулю: 12x²+2x-2 = 0, 2(6x²+x-1) = 0.
Д = 1+24 = 25, х1 = (-1-5)/12 = -1/2, х2 = (-1 + 5)/12 = 4/12 = 1/3.
Найдены 2 критические точки: х1 = (-1/2) и х2 =(1/3).
Находим значения производной на полученных промежутках:
х ∈ ( -∞;(-1/2) ) ((-1/2);(1/3)) ((1/3);+∞).
х = -1 (-1/2) 0 ( 1/3) 1
y' = 8 0 -2 0 12.
Ф_ция ↑ max ↓ min ↑
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
Пошаговое объяснение:
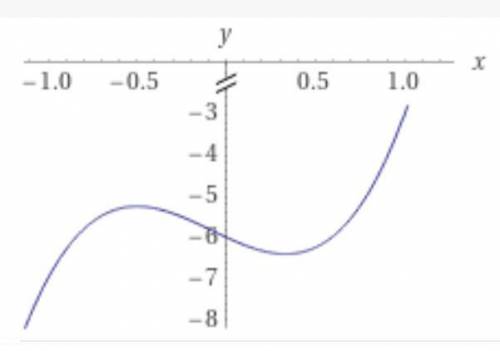
Ну, перво -наперво нужно увидеть, какой график нам дан, в Вашем случае - это график производной ф-ции y = f'(x)
Когда мы ищем точки максимума и минимума (экстремумы ф-ции, xmax, xmin), то должно выполняться условие: f'(x) = 0
Ф-ция возрастает, когда f'(x) > 0,
убывает, когда f'(x) < 0
Максимальные значения ф-ция принимает при подстановке в ф-цию xmax, т.е. fmax (xmax)
Минимальное значения ф-ция принимает при подстановке в ф-цию xmin, т.е. fmin (xmin)
В Вашем случае f'(x) > 0 при х < 2 - т.е. возрастала
f'(x) < 0 при х > 2, точка х = 2 - точка максимума (образуется "горка")
f'(x) + -
2
/ \
точка х = -2 - это так называемая точка перегиба, но ни в коем случае не экстремум, т.к. ф-ция все равно продолжала возрастать.
ответ: только одна точка, х = 2
2.1)35-30=-5;2)75-(-5)=70;3)70*2=140
3.1)4+6=10;2)60:10=6;3)10*3=30