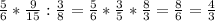
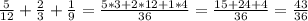
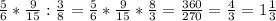
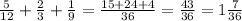
Если число делится на 12, то оно также делится на 3 и на 4. Если число делится на 4, то число, образованное двумя последними цифрами исходного числа, также делится на 4. Поэтому на конце не может быть нечётной цифры, и с конца мы точно вычёркиваем 1. Остаётся 2346214. Число делится на 3, если сумма цифр делится на 3. То есть нужно вычеркнуть ещё две цифры так, чтобы число, образованное двумя последними цифрами исходного числа, также делилось на 4 и при этом сумма цифр числа равнялась 3. Число 14 на 4 не делится, поэтому также обязательно нужно вычеркнуть цифру 1. Теперь будем вычёркивать числа так, чтобы сумма цифр числа делилась на 3. Таким образом, получаем числа 23424, 24624.
ответ: 23424, 24624.
2 Пошаговое объяснение:
Вспомним признак делимости на 25 — число делится на 25, если оно заканчивается на комбинации цифр: 00, 25, 50, 75. Из признака следует, что наше число заканчивается на 75, так как разность этих чисел равна 2. Также ясно, что число не может начинаться с нуля. Наше число принимает вид 1ab75, где исходя из условия становится понятно, что a — 3, тогда b — 5. Запишем искомые числа 13575, 53575, 57575, 97575, 57975, 97975
3.Партнеры сайта:
12 = 3·4.
Для того, чтобы получившееся число делилось на 12, нужно, чтобы оно делилось на 3 и на 4.
Деление на 4 означает, что число четное, а значит последнюю единицу вычеркиваем.
Признак делимости на 3 требует , чтобы сумма цифр числа делилась на 3.
После вычеркивания последней цифры получаем число: 18161512.
Из него надо вычеркнуть еще 2 цифры. Найдем сумму всех оставшихся цифр: 1+8+1+6+1+5+1+2 = 25.
Самые ближайшие суммы, которые делятся на 3 – это 24, 21, 18,...
Чтобы получить, например, в сумме цифр 18 при вычеркивание двух цифр, нужно убрать цифры 6 и 1.
Тогда получится число: 181512. Сумма его цифр равна 1+8+1+5+1+2 = 18. Значит, оно делится на 3.
Проверим, делится ли получившееся число на 4:
181512:4 = 45378.
При деление этого числа на 121 получим:
181512:12 = 15126.
Значит, одно из искомых чисел – это 181512.
4.Число делится на 3, если сумма его цифр делится на 3. Кроме того, сумма цифр должна быть равна их произведению. Кроме того, среди цифр не должно быть цифры 0, иначе произведение цифр будет равно нулю и никогда не будет равным сумме цифр.
Примерами таких чисел могут служить: 11133, 11313, 13113, 31113, 33111, 31311, 31131, 13311, 13131, 11331 и т.д.
ответ: 11133 или 11313 или 13113 или 31113 и т.д.