Пошаговое объяснение:
1) Берешь любые числа, которые подходят, чтобы при х-y = 8
это может быть, как я взяла х = 10, y = 2, может x = 9, тогда y = 1
и доп уравнение было бы x+y= 10
2) Оба уравнения должны быть одинаковыми, тогда и решение у них будет любое
потому что , если сократить 2х-2y = 16
2(x-y) = 16
x-y = 8, как и в условии
т.е ещё варианты: 3x-3y=24, 4x-4y=32 и т.д.
3) система не имеет решений тогда, когда два одинаковых уравнения равны разным числам
т.е. x-y = можно написать любое понравившееся число
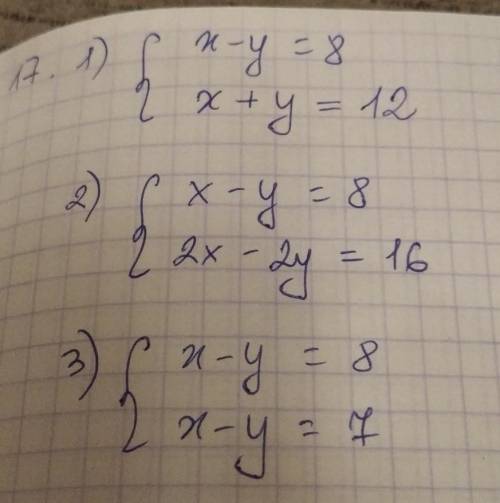
1. Прямая и окружность имеют две общие точки, если расстояние от центра окружности до прямой меньше радиуса окружности.
2. Если прямая АВ - касательная к окружности с центром О и В - точка касания, то прямая АВ и радиус ОВ перпендикулярны.
3. Угол АОВ является центральным, если точка О является центром окружности, а лучи ОА и ОВ пересекают окружность. (отрезки ОА и ОВ будут являться радиусами окружности)
4. Вписанный угол, опирающийся на диаметр, равен 90°.
5. Дано: ∠АСD=31°.
∠ABD = 31° (т.к. он вписанный и опирается на ту же дугу, что и ∠АСD), ∠AOD = 62° (∠AOD центральный и опирается на ту же дугу, что и ∠АСD
. Следовательно он в два раза больше ∠AСD).
6.Если хорды АВ и CD окружности пересекаются в точке Е, то верно равенство
DЕ·ЕС = АЕ·ЕВ.
7.Если АВ- касательная, AD - секущая, то выполняется равенство
АВ² = АD·АС.
8. Если четырехугольник ABCD вписан в окружность, то сумма его противоположных углов равна 180°.
9. Центр окружности, вписанной в треугольник, совпадает с точкой пересечения биссектрис этого треугольника.
10. Если точка А равноудалена от сторон данного угла, то она лежит на биссектрисе этого угла.
11. Если точка В лежит на серединном перпендикуляре, проведенному к данному отрезку, то она равноудалена от концов этого отрезка.
12. Около любого треугольника можно описать окружность.
х-0,3х-0,5х=8
0,2х=8
х=40 км - весь путь