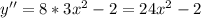
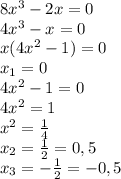
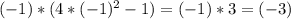 - знак минус
- знак минус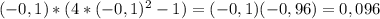 - знак плюс
- знак плюс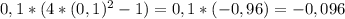 - знак минус
- знак минус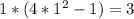 - знак плюс
- знак плюс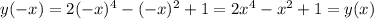 - значит функция четная
- значит функция четная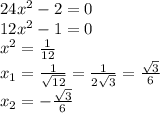
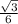 ≈0,289
≈0,289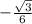 ≈-0,289
≈-0,289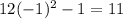 - знак плюс
- знак плюс![[-\frac{\sqrt{3}}{6 };\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4016/e2f5f.png)
![-\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4016/a1cfa.png) и
и 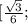 ;+oo)
;+oo)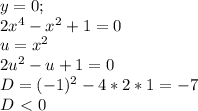
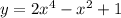
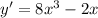
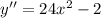
![[-\frac{\sqrt{3}}{6 };\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4016/e2f5f.png)
![-\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4016/a1cfa.png) и
и 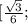 ;+oo)
;+oo)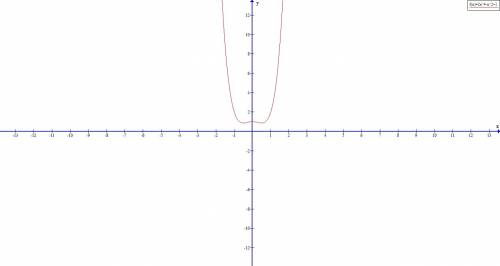
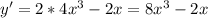
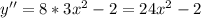
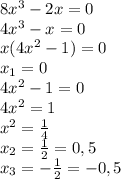
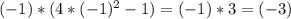 - знак минус
- знак минус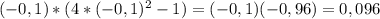 - знак плюс
- знак плюс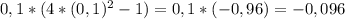 - знак минус
- знак минус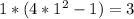 - знак плюс
- знак плюс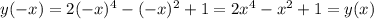 - значит функция четная
- значит функция четная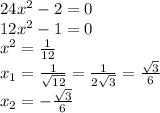
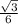 ≈0,289
≈0,289 ≈-0,289
≈-0,289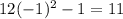 - знак плюс
- знак плюс![[-\frac{\sqrt{3}}{6 };\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4085/e2f5f.png)
![-\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4085/a1cfa.png) и
и 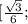 ;+oo)
;+oo)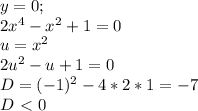
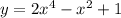
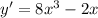
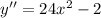
![[-\frac{\sqrt{3}}{6 };\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4085/e2f5f.png)
![-\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4085/a1cfa.png) и
и 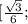 ;+oo)
;+oo)