1. Числа, используемые при счёте.
2. Часть отрезка, ограниченная двумя точками.
4. Переместительный (коммутативный) закон сложения: m + n = n + m . Сумма не меняется от перестановки её слагаемых.
Переместительный (коммутативный) закон умножения: m · n = n · m . Произведение не меняется от перестановки его сомножителей.
Сочетательный (ассоциативный) закон сложения: ( m + n ) + k = m + ( n + k ) = m + n + k . Сумма не зависит от группировки её слагаемых.
Сочетательный (ассоциативный) закон умножения: ( m · n ) · k = m · ( n · k ) = m · n · k . Произведение не зависит от группировки его сомножителей.
Распределительный (дистрибутивный) закон умножения относительно сложения: ( m + n ) · k = m · k + n · k .
5. (a+b)*c=a*c+b*c
6. Уравнение – это равенство, содержащее одну или несколько переменных.
7. Вычислить значение перемннной.
11. Приводим к одному знаменателю. У какой дроби числитель больше числителя другой дроби, та и больше.
15. Работаем с числителями.
1.41
Пошаговое объяснение:
Ну, пусть искомое число - это х,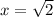 
. Тогда
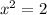
Но мы знаем, что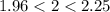 
- это очевидно. Тогда извлечём корень, и в силу его монотонного возрастания, знаки не поменяются. Тогда
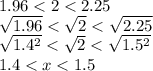
Отлично, мы определили х до первого знака после запятой. Определим его и до второй.
Есть такое число, 1.9881 = 1.41² и 2.0164 = 1.42²
Очевидно, что вот так:
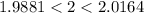
Тогда опять же из-за прекрасной функции корня получаем красивую вещь:
То есть, так как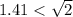 
, то 
, наибольший порядок у у равен порядку 1.41 - а это -2. Тогда у не будет влиять на второй знак после запятой в числе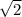 
, тогда 1.41 - десятичная запись 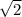до второго знака.
b>7.