10 см² и 5 см²
Пошаговое объяснение:
Рисунок во вложении
Рис . а
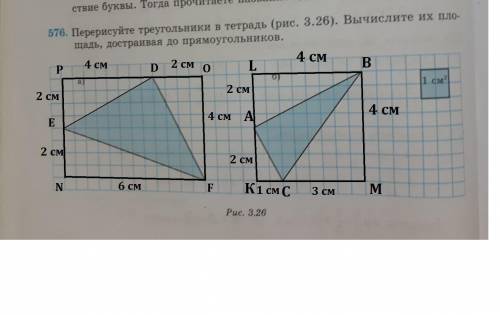
Построим прямоугольник NPOF, который проходит через вершины треугольника EDF.Получили три прямоугольных треугольника EPD,DOF и ENF. Чтобы узнать площадь треугольника EDF(S) надо от площади прямоугольника NPOF(S1) отнять площади треугольников EPD(S2),DOF(S3) и ENF(S4) .Формула площади прямоугольника S=a*b, а формула площади прямоугольного треугольника S=(a*b)/2, где а и b - катеты.
S1=4*6=24 см²
S2=(2*4)/2=4 cм²
S3=(2*4)/2=4 cм²
S4=(2*6)/2=6 cм²
S=S1-S2-S3-S4
S=24-4-4-6=10 см²
Рис.б
Построим прямоугольник КLBM, который проходит через вершины треугольника CAB.Получили три прямоугольных треугольника CKA,ALB и BMC. Чтобы узнать площадь треугольника CAB(S) надо от площади прямоугольника KLBM(S1) отнять площади треугольников CKA(S2),ALB(S3) и BMC(S4) .Формула площади прямоугольника S=a*b, а формула площади прямоугольного треугольника S=(a*b)/2, где а и b - катеты.
S1=4*4=16 см²
S2=(2*1)/2=1 cм²
S3=(2*4)/2=4 cм²
S4=(4*3)/2=6 cм²
S=S1-S2-S3-S4
S=16-1-4-6=5 см²