на плоскости:
1) пролегает мимо окружности
2) пролегает через центр окружности
3) прямая имеет 2 точки касания с окружностью
4) прямая имеет 1 точку касания с окружностью
в мимо окружности в перпендикулярной плоскости
6) мимо окружности под углом к плоскости окружности
7) пролегает через центр окружности в перпендикулярной плоскости
8) пролегает через центр окружности под углом к плоскости окружности
9) прямая имеет 1 точку касания с окружностью в перпендикулярной плоскости
10) прямая имеет 1 точку касания с окружностью под углом к плоскости окружности
11) прямая имеет 1 точку касания с кругом в перпендикулярной плоскости
12) прямая имеет 1 точку касания с кругом под углом к плоскости окружности
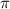в математике, по определению, равно отношению длинны 
произвольной окружности к диаметру 
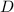той же окружности, поскольку все окружности подобны друг другу, т.е.:
;
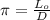формула [1] ;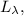
составляющую 
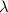часть от длины всей окружности, в данном конкретном случае 
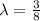от длины всей окружности, то нам просто нужно умножить длину всей окружности на эту самую часть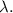 
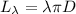формула [2] ;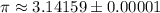
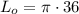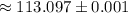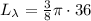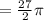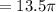см 
см ;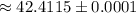
см 
см 
см 
см ;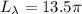
см ;
см .
