обозначим прямоугольник авсд. угол мав=45, угол мсв=30. мв=4. поскольку угол мав=45, то в прямоугольном треугольнике амв угол амв=45. тгда этот треугольник равнобедренный и ав=мв=4. мв/вс=tgмсв. отсюда ад=вс=мв/tg30=4 корня из 3. диагональ вд=корень из (ав квадрат + вс квадрат)=корень из (16+48)=8. мд квадрат=мв квадрат + вд квадрат=16+64=80. амквадрат=мвквадрат + ав квадрат=16+16=32. в треугольнике мад ам квадрат + ад квадрат=32+48=80. но это равно мд квадрат значит мд гипотенуза прямоугольного треугольника мад. аналогично мс квадрат=мв квадрат + вс квадрат=16+48=64. тогда в треугольнике мсд мс квадрат + дс квадрат=64+16=80. и он также прямоугольный. стороны равны ав=дс=4. ад=вс=4 корня из 3. площадь мдс равна s мдс=1/2*мс*дс=1/2*8*4=16.
Площадь полной поверхности правильной треугольной усеченной пирамиды равна сумме площадей её оснований и трех равных боковых граней.
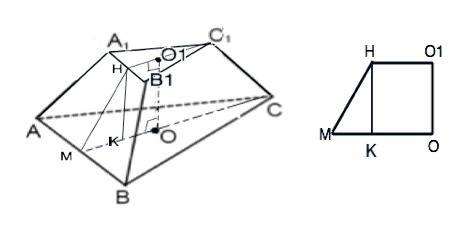
Обозначим вершины фигуры АВСС1А1В1, О и О1 - центры оснований, они же и центры вписанных окружностей. ОО1 - высота пирамиды.
1). Проведем высоты оснований С1Н - в меньшем, СМ - в большем. С1Н=А1С•sin60*=6√3/2=3√3
О1Н=С1Н:3=√3 ( по свойству медиан).
Аналогично СМ=12√3/2=6√3; OM=2√3
2) МНО1О - прямоугольная трапеция.
Проведем НК║ОО1
В ∆ МНК катет НК=ОО1=1, катет МК=МО - НО1=2√3-√3=√3
По т.Пифагора МН=√(НК²+МК²)=√4=2
Площадь боковой грани - площадь равнобедренной трапеции АВВ1А1
S трап=0,5•(a+b)•h
S(АВВ1А1)=0,5•(АВ+А1В1) •HM=0,5•18•2=18 дм²
S( АВС)=12²•√3/4=36√3 дм²
S(A1B1C1)=6²•√3/4=9√3 дм²
S(полн)=3•18+36√3+9√3=27+45√3 дм²
1)
2)
3)
4)