В изобразительном искусстве теме зимы уделяется большое значение. Множество художников видели это время года по-разному и пытались внести в его изображение что-то новое. Одна из картин такого рода – «Февраль. Подмосковье», написанная замечательным живописцем Георгием Нисским. Свою работу художник выполнил маслом.
По названию полотна зрителю становится ясно, что сюжет происходит в последнем месяце зимы где-то под Подмосковьем. На самом деле Нисский писал полотно именно в это время 1954 года.
Изображенная на холсте природа, все еще скованная снегом и льдом, готова вскоре ожить под теплыми весенними лучами. Длинные тени, отбрасываемые от высоких елей, которые ложатся на снег и проезжую часть, говорят о том, что солнце начнет садиться совсем скоро.
Пересекает полотно длинная дорога, уходящая вдаль за линию горизонта, на ней можно заметить несколько машин. Это говорит о том, что трасса не оживленная и находится в небольшом загородном поселке. В тени елей можно заметить строение напоминающее церквушку. Поезд, со множеством составов, двигается по рельсам на возвышающимся холме.
Кажется, что воздух на этой картине тяжелый и влажный, а снег, немного подтаявший и сырой от теплой спокойной погоды. На закате дня небо изображено серо-голубым. По нему плывут тяжелые облака, которые, возможно, принесут на землю последний зимний снег в этом году. В левом углу солнечные лучи окрашивают небосвод розовыми и золотистыми тонами и ярко освещают отдаленный лес впереди, куда уходит дорога.
С живых ярких красок живописец Георгий Нисский мастерски умел придать атмосфере обыденности завораживающее очарование. Его картины наполняют добрыми и светлыми эмоциями своих зрителей. Они учат повсюду видеть красоту, будь то самые простые композиции и пейзажи.
1.Область определения D(x). Неопределенностей типа 0/0 или ∞/∞ - нет.
- Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет.
2. Пересечение с осью Х. Решаем уравнение - Y=0 и находим корни.
 (примерно)
(примерно)
3.Интервалы знакопостоянства:
положительна (между корнями) Х∈(-1.65;1.65)
отрицательна (вне корней) - Х∈(-∞;-1.85)∪(1,65;+∞)
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = -∞
Горизонтальных асимптот - нет.
5. Исследование на чётность. Y(-x) = Y(x).
Функция чётная.
6. Производная функции.Y'(x)= -2*x³+2*x = -2*x*(x²-1)=-2*x*(x-1)(x+1).
Корней - ТРИ. Х1=-1, Х2= 0, Х3 = 1.
Схема знаков производной.
(-∞)__(положит)__(-1)_(отрицат)__(0)_(положит)___ (1)__(отицат__ (+∞)
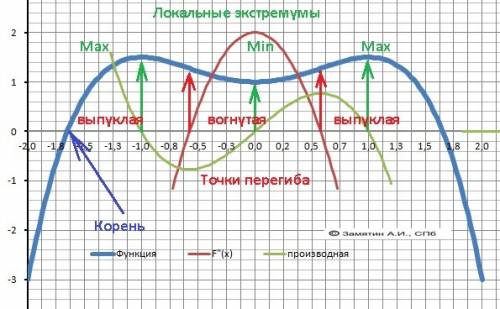
7. Локальные экстремумы. Максимумы – Ymax(-1) = Y(max)(1) = 3/2= 1,5.
Минимум - Ymin(0) = 1.
8. Интервалы монотонности.
Возрастает - Х∈(-∞;-1)∪(0;1), убывает = Х∈(-1;0)∪(1;+∞).
9. Вторая производная - Y"(x) = -6*x²+2 = 1/3 - x².
Корни второй производной - х1= -√3/3 x2= √3/3 -точки перегиба (≈0.58).
10. Выпуклая “горка» Х∈(-∞;-0,58)∪(0,58;+∞),Вогнутая между корнями: Х∈(-0,58;0,58)
10. Область значений Е(у) У∈(-∞;Ymax=1,5)
11. Наклонная асимптота - нет.
12. График в приложении.