Обозначим длины сторон данного прямоугольника через х и у.
Согласно условию задачи, площадь данного прямоугольника равна 24 см^12, следовательно, имеет место следующее соотношение:
х * у = 24.
Также известно, что периметр данного прямоугольника равен 20 см, следовательно, имеет место следующее соотношение:
2 * (х + у) = 20.
Решаем полученную систему уравнений.
Из второго уравнения получаем:
х + у = 20 / 10;
х + у = 10;
у = 10 - х.
Подставляя данное значение у = 10 - х в уравнение х * у = 24, получаем:
х * (10 - х) = 24:
10х - х^2 = 24;
х^2 - 10х + 24 = 0;
х = 5 ± √(25 - 24) = 5 ±√1 = 5 ± 1;
х1 = 5 - 1 = 4;
х2 = 5 + 1 = 5.
Находим у:
у1 = 10 - х1 = 10 - 4 = 6;
у2 = 10 - х2 = 10 - 6 = 4.
– каждому действительному простому корню b соответствует частное решение вида
eᵇˣ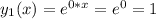
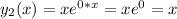
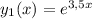
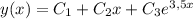
15+8=23
ответ: всего 23 рыбины поймали дети.