Пошаговое объяснение:
Дано:
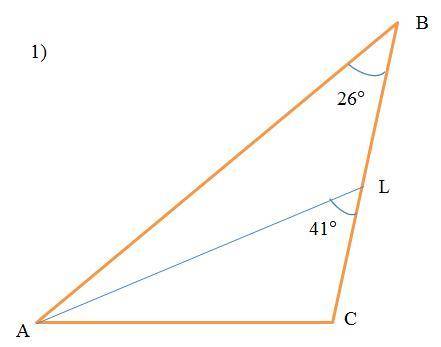
В ΔABC
∠ABC=∠ABL=26°
Уточнение: в условии 1) ∠ALC=41°, а на рисунке 2) ∠LAC=41°. Поэтому задачу решаем для обоих случаев.
Найти: ∠ACB
1) Так как ∠ALC=41°, то смежный с ним ∠ALB=180°-41°=139°.
Используем свойство: сумма внутренних углов треугольника равна 180°:
∠АLB+∠АBL+∠BАL=180°
Отсюда:
∠BAL = 180° - ∠ALB - ∠АBL = 180° - 139° - 26° = 15°.
Биссектриса делит ∠BАC пополам, то
∠BАC = 2·∠BAL = 2·15° = 30°.
Ещё раз используем свойство: сумма внутренних углов треугольника равна 180°:
∠BАC+∠АBC+∠АCB=180°
Отсюда:
∠ACB = 180° - ∠BАC - ∠АBC = 180° - 30° - 26° = 124°.
ответ: ∠ACB = 124°.
2) Так как ∠LAC=41° и биссектриса делит ∠BАC пополам, то
∠BАC = 2·∠LАC = 2·41° = 82°.
Используем свойство: сумма внутренних углов треугольника равна 180°:
∠BАC+∠АBC+∠АCB=180°
Отсюда:
∠ACB = 180° - ∠BАC - ∠АBC = 180° - 82° - 26° = 72°.
ответ: ∠ACB = 72°.
Пошаговое объяснение:
2у - х = 7;
х^2 - xy - y^2 = 20;
Решение данной системы уравнений будем искать подстановки, выразим в первом уравнении переменную х через у.
х=2у-7;
х^2 - xy - y^2 = 20;
Подставляем выражение переменной х во второе уравнение.
(2у-7)^2-(2у-7)y-y^2=20;
Применяем в левой части формулу сокращенного умножения (квадрат двучлена) и раскрываем скобки.
4y^2-28y+49-2y^2+7y-y^2=20;
y^2-21y+29=0;
D=b^2-4ac=(-21)^2-4*29=441-116=325;
y1=(-b-√D)/2a=(21-√325)/2=(21-5√13)/2;
y2=(-b+√D)/2a=(21+√325)/2=(21+5√13)/2;
x1=2*(21-5√13)/2-7=14-5√13;
x2=2*(21+5√13)/2-7=14+5√13;
ответ:(14-5√13;(21-5√13)/2),(14+5√13;(21+5√13)/2)
35/56=5/8
72/81=8/9