Скорость первого принимаем за у км/ч.
Скорость второго (у+4) км/ч.
Время второго t, время первого t+2/3.
Время в минутах переводим в часы: 49 минут = 2/3 часа.
Выполнив условия задачи, составим уравнение, учитывая расстояние:
42/у - 42/(у+4) = 2/3
сводим к общему знаменателю, получим квадратное уравнение:
у²+4у-252=0
D=1024
√D = 32
у1=(-4+32)/2 = 14 (км/ч) - скорость первого.
у2 = (-4-32) /2 = -18 (отрицательное число не подходит для скорости)
14+4 = 18 (км/ч) - скорость второго.
ответ: скорость второго велосипедиста 18 км/ч.
-15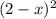
Пошаговое объяснение:
Самый простой — через уравнение и теорему Виета
-60 + 60x - 15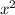
= 0
D =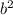 
- 4ac = 
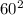- 4·(-15)·(-60) = 3600 - 3600 = 0
Т. к. дискриминант равен 0, квадратное уравнение имеет один действительный корень:
x =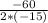 
= 2
По теореме Виета -60 + 60x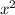 - 15 = -15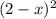
Но у меня подозрение, что это вы ещё не проходили, так что считайте всё вышесказанное проверкой правильности этого решения:
Вынесем -15:
-15(4 - 4x + )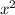
Сгруппируем
-15((4 - 2x)(-2x + ))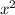
Выносим за скобки 4 и x соответственно:
-15(2(2 - x) - x(2 - x)) <=> -15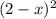
4*2^(2x)+19*2^(x)-5=0
4*(2^(x))^2+19*2^(x)-5=0
пусть t=2^(x)
Тогда 4*t^2+19*t-5=0
D=441
t1=-5 t2=1/4
При t=-5 нет решений, т. к. 2>0 и следовательно 2^(x)>0, а 5<0.
Далее решаем уравнение:
t=1/4
2^(x)=1/4
x=-2
ответ: -2.