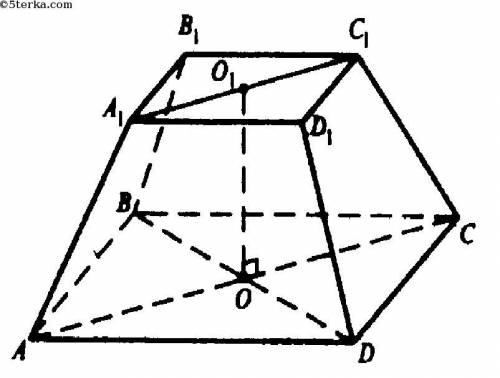
Пусть дана правильная четырехугольная усеченная пирамида 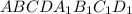 , где
, где 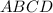 и
и 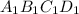 — квадраты со сторонами соответственно 22 см и 6 см. Боковое ребро пирамиды
— квадраты со сторонами соответственно 22 см и 6 см. Боковое ребро пирамиды 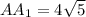 см.
см.
Найдем площадь 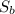 боковой поверхности заданной пирамиды.
боковой поверхности заданной пирамиды.
Для того чтобы ее найти, следует найти площадь одной боковой грани (равнобедренной трапеции) и ее умножить на 4.
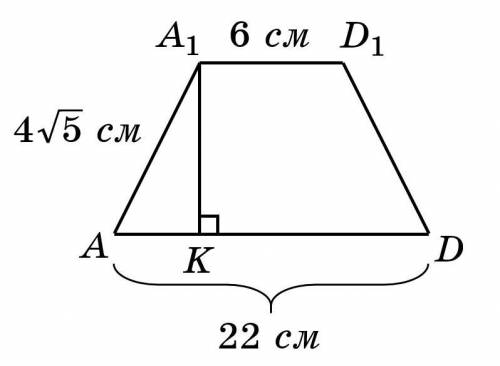
Рассмотрим равнобедренную трапецию 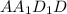
Проведем в трапеции высоту 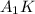
Найдем 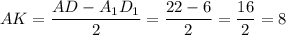 см
см
Рассмотрим прямоугольный треугольник 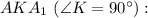
По теореме Пифагора: 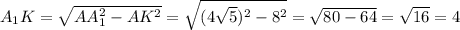 см.
см.
Следовательно, площадь трапеции равна
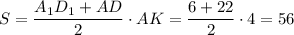 см².
см².
Таким образом, 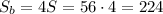 см².
см².
ответ: 224 см².
-8,5<x<-7,25
Переносим через неравенство -8,5, когда переносим через неравенства или через равно минус меняется на плюс, а разделить на умножить.
1) x<8,5-7,25
x<1,25
2)-0,5<x<0,1
x<0,5+0,1
x<0,6
3)-3/10<x<1/5
-3/10-1/5<x
x<1/5