3.
Пошаговое объяснение:
Найдем область допустимых значений. Так как арифметический квадратный корень определен на множестве неотрицательных чисел, то найдем ОДЗ, решив систему неравенств.
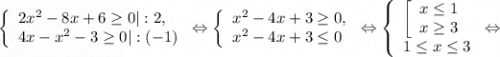
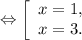
Решим отдельно каждое неравенство методом интервалов.
Рассмотрим функцию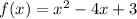 
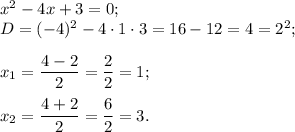
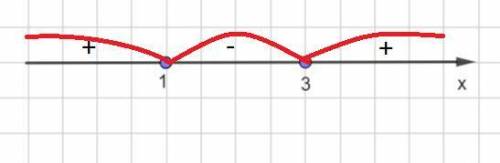
Определим знак функции на каждом интервале и получим:
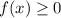x∈ (-∞; 1]∪[3; +∞)
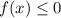x∈[1; 3]
Данная системе имеет решение только, если х=1 и х=3.
Проверим каждое значение:
x=1
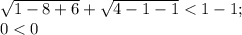
неверно
x=3
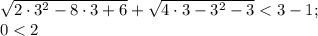
Данное неравенство верно. Значит, решение заданного неравенства является х=3
Пошаговое объяснение:
1) Докажем, что квадрат натурального числа не может дать в остатке 2 при делении на 3
а≡0(mod 3)⇒a²≡0(mod 3)
а≡(±1)(mod 3)⇒a²≡(±1)²≡1(mod 3)
x²+y²-z²=0≡0(mod3) значит по крайней мере одно из чисел x, y, z должно делится на три. Из чего следует делимость на три числа xyz
2) Пусть xyz не делится на 5. Тогда ни одно из чисел x, y, z не делится на 5
а≡0(mod 5)⇒a²≡0(mod 5)
а≡(±1)(mod 5)⇒a²≡(±1)²≡1(mod 5)
а≡(±2)(mod 5)⇒a²≡(±2)²≡4≡-1(mod 5)
Значит, если ни одно из чисел x, y, z не делится на 5, то должно выполнится равенство
x²+y²-z²≡±1±1±1≡0(mod 5)
А это не возможно.
3) Если среди чисел x, y, z по крайней мере два четных, или есть одно делящееся на 4 тогда xyz делится на 4. Пусть их будет не более одного и это чётное число не делится на 4.
То что в равенстве x²+y²=z² все три числа x, y, z не могут быть нечетными очевидно.
Остается рассмотреть случай того что среди чисел x, y, z одно четное не делящееся на 4
а) x, y- нечётные, z-чётное
x=2n+1, y=2k+1, z=2m
x²+y²=(2n+1)²+(2k+1)²=4(n²+n+k²+k)+2≡2(mod4)
z²=(2m)²=4m²≡0(mod4)
Равенство не возможно.
б) одно из чисел x, y не чётные, другое нечётное, z-нечётное
(2n+1)²+(2m)²=(2k+1)², m-не делится на 2
m²=k²+k-n²-n=(k-n)(k-n+1)
Но числа (k-n) и (k-n+1) разной чётности. Значит одно из них чётно.
Тогда и число m² чётно⇒m-чётное.
Получили противоречие.
Значит делится на 4
Ч.т.д.
2)у= –2х^2–12х–18=х^2+6х+9. Х=3
3)у=(х–3)(х+3). Х=–3 и 3
4)у=х^2–10х+9. Х= 9 и 1