1). S полн. пов =2112 см^2
2). f'(π)=-5
Пошаговое объяснение:
1).
ABCDA1B1C1D1 - прямая призма
ABCD - ромб
=> призма правильная
AC_|_ BD, O- точка пересечения диагоналей
AC=12 см
BD=16 см
1). рассмотрим прямоугольный треугольник АОВ:
<О=90°
АО=6 см - катет
ВО=8 см - катет
АВ - гипотенуза, найти по теореме Пифагора:
АВ^2=АО^2+ВО^2
АВ^2=100
2). рассмотрим прямоугольный треугольник АВА1:
<А =90°
АВ- катет
АА1 - катет
А1В - гипотенуза - диагональ боковой грани призмы
теорема Пифагора:
(А1В)^2=АВ^2+(А1А)^2
26^2=100+(А1А)^2
А1А= 24 см
Sполн.пов=Sбок.пов+2S осн
S полн.пов=Р осн ×Н+2×(1/2) ×АС×BD
S полн пов=4×10×24+2×(1/2)×12×16=1920+192=2112
2).
f'(x)=(tg5x)'=
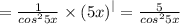
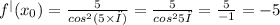
ответ: 20√3см²
Пошаговое объяснение: При проведении высот с вершины углов меньшего основания, образуется прямоугольник и два прямоугольных треугольника. Углы при меньшем основании равны: 150-90=60°. Тогда углы при большем основании равны: 90-60=30°. Гипотенузой этих треугольников являются боковые стороны трапеции, а катетами высота трапеции и разность между нижним и верхним основаниями.
Находим высоту трапеции: она будет равна половине гипотенузы, так как лежит против угла 30° и равна: h=8/2=4см
По теореме Пифагора находим второй катет треугольника
а=√8²-4²=√64-16=√48=4√3см
Находим меньшее основание трапеции: 9√3-2*4√3=9√3-8√3=√3смНаходим среднюю линию трапеции: (9√3+√3)/2=10√3/2=5√3смНаходим площадь трапеции: S=5√3*4=20√3cм²
г) -14-(-15)=1;
Е) 35-(-40)=75;
З) -35-(-40)=5.