Втреугольнике авс сн-высота, аd- биссектриса, о-точка пересечения прямых сн и ad, угол bad=37 градусов. найдите угол аос.

👇

Увидеть ответ

Ответ:

Сирунс

04.01.2021

<BAD=37°
<CHA=90°
<AOH+<BAD+<CHA=180°
<AOH=180°-37°-90°
<AOH=53°
<AOC+<AOH=180°
<AOC=180°-<AOH=180°-53°=127°

4,7(90 оценок)

Открыть все ответы

Ответ:

dbuzoverova

04.01.2021

1) Из условия SB=SD и СВ = СD как стороны ромба следует, что отрезок SС лежит в вертикальной плоскости.
Теперь рассмотрим треугольник АSС.
Отрезок АС, как диагональ ромба с острым углом 60 градусов, равен:
АС = 2*8*cos (60°/2) = 16*(√3/2) = 8√3.
AC² = 192, SC² = 33. Их сумма равна 225, то есть равна АS² = 15² = 225.
Поэтому угол SСА прямой и отрезок SС - высота пирамиды.

2) Задачу определения угла между плоскостью ASC и ребром SB можно решить двумя
2.1) При геометрическом методе нужно найти какую-нибудь удобную точку на прямой, опустить перпендикуляр на плоскость, выяснить, что из себя представляет проекция, а потом решать планиметрическую задачу по поиску угла φ в треугольнике.
Спроецируем ребро SB на плоскость ASC.
Точка S остаётся на месте, а точка В - в точку О (это середина диагонали АС основания).
Находим длину отрезка SO = √(SC²+OC²) = √(33+48) = √81 = 9.
Тогда заданный угол - это угол BSO.
Треугольник BSO - прямоугольный так как отрезок ВО перпендикулярен плоскости ASC.
Получаем ответ: угол BSO = arc tg (4/9) = 0,418224 радиан = 23,96249°.

2.2) При алгебраическом методе вводится система координат, определяются координаты двух точек на прямой и уравнение плоскости, а затем применяется формула вычисления угла между прямой и плоскостью.
Вводим систему координат: точка А - начало, ось Оу по диагонали АС, ось Ох - перпендикулярно Оу, ось Oz - через точку А.
Координаты точки В(-4; 4√√3; 0), точки S(0; 8√3; √33).
Вектор SB(-4; -4√3; -√33), модуль |SB| =√(-4)²+(-4√3)²+(-√33)²) = √97.
Так как плоскость ASC совпадает с плоскостью zOy, то её уравнение х = 0, коэффициент А = 1.
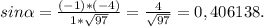
$sin \alpha = \frac{(-1)*(-4)}{1* \sqrt{97}} = \frac{4}{ \sqrt{97} }=0,406138.$
Угол BSO = arc sin (4/√97) = 0,418224 радиан = 23,96249°.

4,5(9 оценок)

Ответ:

Viktoria1289

04.01.2021

Угол В тупой, может быть только при вершине; проведем биссектрису и высоту ВВ1; проведем высоту АА1 на продолжение стороны СВ; угол АА1В=90гр.; продолжим биссектрису В1В и высоту АА1 до пересечения в т. Д; в тр-ке АВС уголВАВ1=(180-110):2=35 гр.; в тр-ке АА1В уг.АВА1=180-110=70гр.(смежный с уг.В); в тр-ке АА1В уг. А1АВ=90-70=20гр. (по св-ву острых углов прямоуг. тр-ка; отсюда уг. А1АВ1=35+20=55гр.; в прямоуг. тр-ке АДВ1 искомый уг. Д между биссектрисой В1Д и высотой АД=90-55=35гр. (по св-ву острых углов прямоуг. тр-ка.) ответ: 35гр.

4,4(58 оценок)

Это интересно:

Стиль-и-уход-за-собой

23.06.2021

10 лучших способов улучшить состояние кожи...

Финансы-и-бизнес

24.07.2022

11 проверенных способов, как дополнительно заработать в свободное время...

Транспорт

14.07.2022

Как быстро и легко отчистить жевательную резинку от сидения...

Компьютеры-и-электроника