ответ
1) Пусть 160 кг сплава составляют 100%. Примем, что 72 кг олова в этом сплаве составляют х%.
2) Сделаем запись:
160 кг — 100%;
72 кг — х%.
3) Составим и решим пропорцию:
160 : 72 = 100 : х;
160 * х = 72 * 100;
160х = 7200;
х = 7200 : 160;
х = 45.
Значит, в первом сплаве содержание олова составляет 45%.
2) Вычислим содержание олова во втором сплаве.
240 кг — 100%;
108 кг — х%.
240 : 108 = 100 : х;
240х = 108 * 100;
240х = 10800;
х = 10800 : 240;
х = 45.
Находим, что и во втором сплаве содержание олова составляет 45%.
ответ: одинаково
Пошаговое объяснение:
Вспоминаем свойства степеней, это алгебра 7-го класса. Фото внизу.
Задача 497.
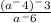
В этом примере необходимо раскрыть скобки. Св-во степени: при раскрытии скобок показатели степеней перемножаются.
Получаем:
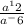
При делении показатели степеней вычитаются!
Получаем:
a^12 - (-6) = a^12+6 = a^18 (^ - степень).
Задача №498. (Попробуй решить самостоятельно).
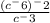
Тут опять же раскрытие скобок и деление. (Свойства при раскрытии скобок и делении выше!).
Получаем: c^12-(-3) = c^15 (^ - степень!)
Задача 499.
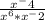
Тут для начала надо разобраться с знаменателем дроби: при умножении степени складываются.
Получаем:
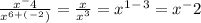
Задача 500.
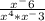
Производим манипуляции со степенями в знаменателе(степени при умножении складываются) и получаем:
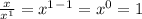
И вот тут еще одно свойство степеней: число, которое возводят в нулевую степень, будет всегда равно единице.
Задача 501.
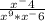
И опять мы делаем свои дела в знаменателе, получаем дробь:
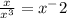
Задача 502.
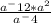
Делаем свои дела уже в числителе. Получим дробь:
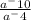 = a^-6
= a^-6
Не забудь, что при делении степени вычитаются!

Пятикратные числа: 15; 45; 60; 105; 135; 225 и 270
15 : 5 = 3; 45 : 5 = 9; 60 : 5 = 12; 105 : 5 = 21; 225 : 5 = 45; 270 : 5 = 54
Простое число: 3 (нет простых множителей, кроме 1 * 3)
Сложное число: 9; 12: 21: 45; 54 (их можно разложить на простые множители)
Девятикратные числа: 45; 135; 225 и 270
45 : 9 = 5; 135 : 9 = 15; 225 : 9 = 25; 270 : 9 = 30
Простое число: 5 (нет простых множителей, кроме 1 * 5)
Сложное число: 15; 25; 30 (их можно разложить на простые множители)