24
Пошаговое объяснение:
Обозначим первую цифру числа за х, а вторую за y. Зная, что число у нас двузначное, х будет числом десятков, а у - числом единиц, то есть наше число равно 10х+у.
Сумма цифр - это х+у. Она в четыре раза меньше 10х+у, запишем уравнение:
10х+у=4(х+у)
10х+у=4х+4у
Перенесем все в левую часть:
10х+у-4х-4у=0
6х-3у=0
Сократим на 3:
2х-у=0
у=2х
Произведение цифр числа - это х*у. Если прибавить его к нашему числу 10х+у, мы получим 32. Запишем уравнение:
10х+у+х*у=32
Заменим у на найденные в предыдущем уравнении 2х:
10х+2х+2х*х=32
2х^2+12х=32
Перенесем все в левую часть и получим квадратное уравнение:
2x^2+12x-32=0
Сократим на 2:
x^2+6x-16=0
D=36+64=100
x1,2=(-6+-10)/2
x1=-8, х2=2. Отрицательные числа нам не подходят, таким образом, х=2. у=2х, тогда у=2*2=4.
Наше число - 24. Проверим: сумма цифр 2+4=6, 24/6=4. Действительно в 4 раза больше суммы цифр. 24+2*4=24+8=32, действительно равно 32. Все в порядке.
ответ: 24
507. Дано: ΔABC, CH і AT — висоти, AB = 8 см, ВС = 6 см, СН = 3 см. Знайти АТ.
Площа трикутника рівна половині добутку сторони на висоту, проведену на цю сторону.
Знайдемо площу трикутника ΔABC:
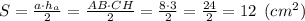
Виразимо іншу висоту через цю ж формулу:
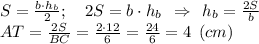
Відповідь: АТ = 4 см.
508. Дано: ΔEFS — рівнобедрений, EF — основа, EF = 40 см, SF = 29 см. Знайти S(EFS).
SF = SE = 29 см, так як ΔEFS — рівнобедрений.
Проведемо висоту SH до основи тр-ка. Висота у рівнобедреному тр-ку є медіаною, тому EH = FH = 40/2 = 20 см.
Знайдемо катет SH з ΔESH (∠EHS = 90°) за т. Піфагора:
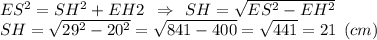
Підставимо значення у формулу площі трикутрина:
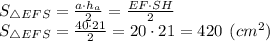
Відповідь: Площа ΔEFS рівна 420 см².
