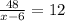
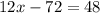
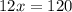
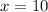
В решении.
Пошаговое объяснение:
55.
а) х - 12 < 0
x - 12 + 12 < 0 + 12
x < 12
Решение неравенства х∈(-∞; 12).
Неравенство строгое, скобка круглая, а у знаков бесконечности скобка всегда круглая.
На числовой прямой штриховка вправо от - бесконечности до 12.
г) х - 1/2 < 4
x - 0,5 < 4
x - 0,5 + 0,5 < 4 + 0,5
x < 4,5
Решение неравенства х∈(-∞; 4,5).
Неравенство строгое, скобка круглая, а у знаков бесконечности скобка всегда круглая.
На числовой прямой штриховка вправо от - бесконечности до 4,5.
ж) х - 4,2 >= 8
x - 4,2 + 4,2 >= 8 + 4,2
x >= 12,2
Решение неравенства х∈[12,2; +∞).
Неравенство нестрогое, скобка квадратная, а у знаков бесконечности скобка всегда круглая.
На числовой прямой штриховка вправо от 12,2 до + бесконечности.
56.
а) x + 4 <= 5
x + 4 - 4 <= 5 - 4
x <= 1
Решение неравенства х∈(-∞; 1].
Неравенство нестрогое, скобка квадратная, а у знаков бесконечности скобка всегда круглая.
На числовой прямой штриховка вправо от - бесконечности до 1.
г) у - 7 и 1/2 > -7
y - 7,5 > -7
y - 7,5 + 7,5 > -7 + 7,5
y > 0,5
Решение неравенства х∈(0,5; +∞).
Неравенство строгое, скобка круглая, а у знаков бесконечности скобка всегда круглая.
На числовой прямой штриховка вправо от 0,5 до +бесконечности.
ж) z - 4,5 <= -0,2
z - 4,5 + 4,5 <= -0,2 + 4,5
z <= 4,3
Решение неравенства х∈(-∞; 4,3].
Неравенство нестрогое, скобка квадратная, а у знаков бесконечности скобка всегда круглая.
На числовой прямой штриховка вправо от - бесконечности до 4,3.