4целых 2\3x+3 целых5/14=6целых 11/21 решить уравнение

👇

Увидеть ответ

Ответ:

рвовттатс

04.06.2020

4,2/3Х+3.5/14=6.11/21

14/3Х=137/21-47/14=274/42-141/42=133/42

Х=133/42:14/3=133/42 х 3:14=133/14 х 1:14

Х=133/196

4,8(6 оценок)

Ответ:

akow08

04.06.2020

4 2/3х+3 5/14=6 11/21
4 2/3х=6 11/21-3 5/14
4 2/3х=3 1/6
Х=3 1/6:4 2/3
Х=19/28

4,8(56 оценок)

Открыть все ответы

Ответ:

SweetDreamsOfMade

04.06.2020

$\begin{cases} [x]+\{y\}=-2.13\\ [y]+\{x\}=3.5\end{cases}$

Отметим области значений для функции целой и дробной части:

$y=[x];\ E(y)=\mathbb{Z}$

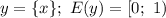
$y=\{x\};\ E(y)=[0;\ 1)$

Выразим из первого уравнения целую часть числа "х":

$[x]=-2.13-\{y\}$

Зная оценку для дробной части числа, оценим правую часть:

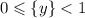
$0\leqslant \{y\} < 1$

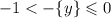
$-1 < -\{y\}\leqslant0$

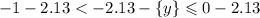
$-1-2.13 < -2.13-\{y\}\leqslant0-2.13$

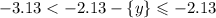
$-3.13 < -2.13-\{y\}\leqslant-2.13$

Так как правая часть равна левой, то можем переписать:

$-3.13 < [x]\leqslant-2.13$

Но [x] - это целое число. Единственное целое число, подпадающее в промежуток $(-3.13;\ -2.13]$ - это число -3.

Таким образом:

[x]=-3

Тогда, выражая второе неизвестное из первого уравнения, получим:

$\{y\}=-2.13-[x]$

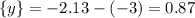
$\{y\}=-2.13-(-3)=0.87$

Аналогичные действия проделаем со вторым уравнением. Сначала выразим целую часть числа "у":

$[y]=3.5-\{x\}$

Оценим правую часть:

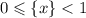
$0\leqslant \{x\} < 1$

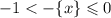
$-1 < -\{x\}\leqslant0$

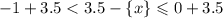
$-1 +3.5 < 3.5-\{x\}\leqslant0+3.5$

$2.5 < 3.5-\{x\}\leqslant3.5$

Так как правая часть равна левой, то:

$2.5 < [y]\leqslant3.5$

Единственное целое число, подпадающее в промежуток $(2.5;\ 3.5]$ - это число 3:

[y]=3

Выражаем второе неизвестное из второго уравнения:

$\{x\}=3.5-[y]$

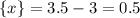
$\{x\}=3.5-3=0.5$

Остается найти сами числа "х" и "у". Для этого представим их в виде суммы своих целой и дробной частей:

$x=[x]+\{x\}=-3+0.5=-2.5$

$y=[y]+\{y\}=3+0.87=3.87$

ответ: (-2.5; 3.87)

4,4(89 оценок)

Ответ:

anyadorr

04.06.2020

900

Пошаговое объяснение:

Всего имеется 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

По условию, цифры 4, 5, 6, 8 не используются в задаче.

У нас осталось 6 цифр: 0, 1, 2, 3, 7, 9

Из этих шести цифр составляеи пятизначные числа, делящиеся на 4.

Признак делимости на 4: число делится на 4, если две последние его цифры нули или составляют число, делящееся на 4, т.е. последними двумя цифрами числа могут быть 00, 12, 20, 32, 92 - всего 5 вариантов. Тогда для выбора первой цифры пятизначного числа существует 5 вариантов - все разрешенные в задаче цифры, кроме нуля. Для выбора следующих двух цифр на место сотен и тысяч можно выбрать любую цифру из 6-ти имеющихся. Полученные варианты перемножаем и получаем количество искомых пятизначных чисел:

5*6*6*5 = 900

4,6(6 оценок)

Это интересно:

Компьютеры-и-электроника

09.10.2022

Как сделать стекло в игре Minecraft: подробный гайд...

Здоровье

14.01.2023

Очистка организма от кокаина: научно проверенные методы...

27.05.2020

Как добиться ясности ума: советы от экспертов...

Дом-и-сад