Меры безопасности при движении на легковом автомобиле
Самым ответственным лицом за соблюдение правил поведения в легковом автомобиле является водитель, основное внимание которого должно быть направлено на обеспечение безопасности окружающих людей. Водитель автомобиля несёт ответственность за соблюдение техники безопасности пассажирам, он должен следить за наличием в машине полностью укомплектованной аптечки, огнетушителя и лично соблюдать и технику безопасности и правила по охране труда.
В легковом автомобиле разрешена перевозка такого количества людей, сколько оборудованных для их посадки мест имеется в стандартной комплектации, причём пассажиры не должны мешать водителю авто управлять им, также они не должны ограничивать обзорность. Правила поведения в легковом автомобиле категорически запрещают перевозить пассажиров в багажном отделении, есть, курить, употреблять алкогольные напитки во время езды, открывать и закрывать двери автомобиля, находящегося в движении.
Одной из основных проблем современных автолюбителей является неразрешённое использование мобильных телефонов. Во время езды на автомобиле категорически запрещено разговаривать по мобильному телефону во избежании создания аварийной ситуации на дороге. Если же телефонный разговор является очень важным, необходимо остановить автомобиль на дорожной обочине и осуществить разговор, и только после этого можно продолжать движение. Телефонные разговоры за рулем могут вызвать непредсказуемую психологическую реакцию у водителей автомобиля, тем самым отвлекая его от управления транспортным средством.
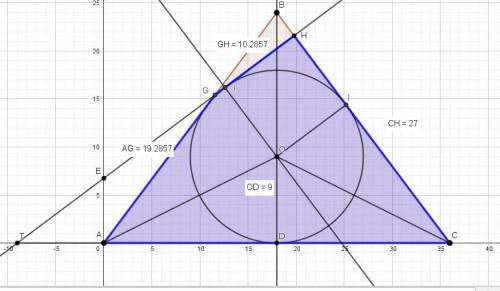
Так как три стороны искомого четырёхугольника – это стороны исходного треугольника, то вписанная в четырёхугольник окружность является и вписанной в треугольник.
То есть такая окружность – единственная и её радиус определяется размерами треугольника.
Радиус окружности r = S/p.
Площадь треугольника определяем по формуле Герона.
Полупериметр р = (30+30+36)/2 = 96/2 = 48.
S = √(p(p-a)(p-b)(p-c)) = √(48*18*18*12) = √186624 = 432 кв.ед.
Получаем r = 432/48 = 9.
Заданная прямая, образующая четырёхугольник, это касательная к окружности и перпендикулярная боковой стороне.
Длина отрезка СН = 18 + 9 = 27.
Находим тригонометрические функции угла С.
Определяем высоту BD = 2S/AC = 2*432/36 = 24.
sin C = 24/30 = 4/5, cos C = 18/30 = 3/5, tg C = 24/18 = 4/3.
Находим координаты точки Н.
x(H) = 36 – 27*cos C = 36 – (27*3/5) = 99/5 = 19,8.
y(H) = 27*sin C = 27*(4/5) = 108/5 = 21,6.
Координаты точки G находим как точку пересечения прямых AB и GH.
Уравнение АВ: у = (4/3)х.
Уравнение ВС: у = (-4/3)х + (36*4/3) = (-4/3)х + 48.
Угловой коэффициент к перпендикулярной прямой GH равен: к = -1/(-4/3) = 3/4.
Уравнение GH: y = (3/4)x + b. Для определения параметра b подставим координаты точки Н: 21,6 = (3/4)*19,8 + b, отсюда b = 6,75.
Уравнение GH: y = (3/4)x + 6,75.
Приравниваем (4/3)x = (3/4)x + 6,75.
Получаем x(G) = 81/7, y(G) = 108/7.
Имея координаты четырёх точек находим площадь искомого четырёхугльника.
Примем условные координаты точек.
Площадь треугольника ABC
S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 27,77143
Площадь треугольника ACD 388,8
Площадь четырёхугольника АBCD S(ABCD)= 416,5714.
S(AGHC)= 416,5714.
200 человек - х
х=160000
800/430=1,9/1, а значит
160000/1,9=84210,5