Пусть событие А - изделие окажется бракованным и рассмотрим гипотезы :
H_1-H
1
− изделие изготовлено первым поставщиком;
H_2-H
2
− изделие изготовлено вторым поставщиком;
H_3-H
3
− изделие изготовлено третьим поставщиком
Из условия P(H_1)=\dfrac{200}{1000}=0.2;~ P(H_2)=\dfrac{300}{1000}=0.3;~ P(H_3)=\dfrac{500}{1000}=0.5P(H
1
)=
1000
200
=0.2; P(H
2
)=
1000
300
=0.3; P(H
3
)=
1000
500
=0.5 и условные вероятности
\begin{gathered}P(A|H_1)=5\%:100\%=0.05\\ P(A|H_2)=6\%:100\%=0.06\\ P(A|H_3)=4\%:100\%=0.04\end{gathered}
P(A∣H
1
)=5%:100%=0.05
P(A∣H
2
)=6%:100%=0.06
P(A∣H
3
)=4%:100%=0.04
По формуле полной вероятности, вероятность получения со склада бракованного изделия равна
\begin{gathered}P(A)=P(A|H_1)P(H_1)+P(A|H_2)P(H_2)+P(A|H_3)P(H_3)=\\ \\ =0.2\cdot 0.05+0.3\cdot 0.06+0.5\cdot 0.04=0.048\end{gathered}
P(A)=P(A∣H
1
)P(H
1
)+P(A∣H
2
)P(H
2
)+P(A∣H
3
)P(H
3
)=
=0.2⋅0.05+0.3⋅0.06+0.5⋅0.04=0.048
Тогда вероятность получения со склада годного изделия равна
\overline{P(A)}=1-P(A)=1-0.048=0.952
P(A)
=1−P(A)=1−0.048=0.952
ответ: 0,952.
В классе всего 12 + 18 = 30.
1) Вероятность выбрать первого мальчика равна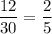 
. Одного человека мы выбрали уже, тогда в классе остается 11 мальчиков и 18 девочек. Вероятность выбрать второго мальчика равна 
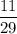. По теореме умножения, искомая вероятность: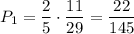 
2) Выбрать первую девочку можно с вероятностью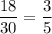 
. В классе остается 29 человек из них 17 девочек. Вероятность выбрать вторую девочку равна 
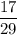. По теореме умножения, искомая вероятность: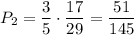 
3) Вероятность того, что среди двух выбранных человек окажутся девочка и мальчик, равна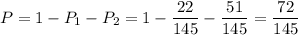 
ответ: 1) 22/145; 2) 51/145; 3) 72/145.
2)Латинский язык имеет и большое общеобразовательное значение, так как лучше и глубже анализировать русский язык, в который перешли многие латинские корни, создав ряд новых слов, например: коммунизм, президиум, консилиум, кворум, университет и т. д.